
已知函数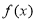 定义在
定义在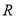 上,对任意的
上,对任意的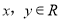 ,
,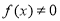 ,且
,且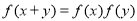 .
.
(1)求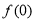 ,并证明:
,并证明: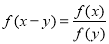 ;
;
(2)若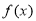 单调,且
单调,且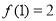 .设向量
.设向量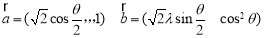 ,对任意
,对任意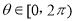 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)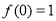 (2)
(2)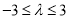
【解析】
试题分析:(1)借助于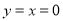 特殊值得
特殊值得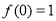 ,然后把
,然后把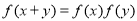 变形
变形
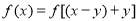 =
= 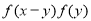 即可,(2) 首先判断出函数
即可,(2) 首先判断出函数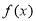 是增函数,然后找出
是增函数,然后找出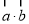 ,代入
,代入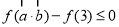 整理的
整理的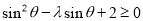 ,最后用分类讨论的思想方法求出
,最后用分类讨论的思想方法求出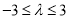 即可.
即可.
(1)令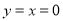 得
得 ,又∵
,又∵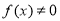 ,
,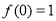 , 2分
, 2分
由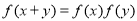 得
得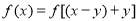 =
=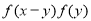 ,
,
∵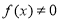 ,∴
,∴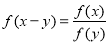 . 5分
. 5分
(2) ∵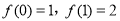 ,且
,且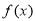 是单调函数,∴
是单调函数,∴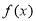 是增函数. 6分
是增函数. 6分
而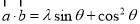 ,∴由
,∴由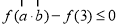 ,得
,得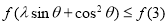 ,
,
又∵因为 是增函数,∴
是增函数,∴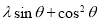
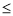
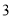 恒成立,
恒成立,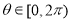 .
.
即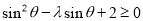 . 8分
. 8分
令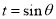 ,得
,得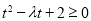 (﹡).
(﹡).
∵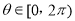 ,∴
,∴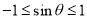 ,即
,即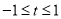 .
.
令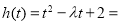
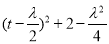
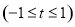 , 10分
, 10分
①当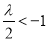 ,即
,即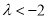 时,只需
时,只需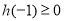 ,(﹡)成立,
,(﹡)成立,
∴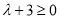 ,解得
,解得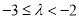 ; 11分
; 11分
②当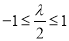 ,即
,即 时,只需
时,只需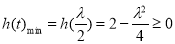 ,(﹡)成立,
,(﹡)成立,
∴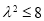 ,解得
,解得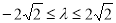 ,∴
,∴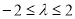 . 12分
. 12分
③当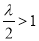 ,即
,即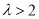 时,只需
时,只需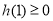 ,(﹡)成立,
,(﹡)成立,
∴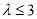 , ∴
, ∴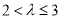 , 13分
, 13分
综上,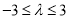 . 14分
. 14分
考点:抽象函数;函数的单调性;向量的数量积公式;不等式恒成立的问题;分类讨论的思想方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016届山东省威海市乳山市高一下学期期末数学试卷(解析版) 题型:选择题
下列说法中不正确的是( )
A.对于线性回归方程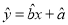 ,直线必经过点
,直线必经过点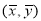
B.茎叶图的优点在于它可以保存原始数据,并且可以随时记录
C.将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变
D.掷一枚均匀硬币出现正面向上的概率是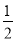 ,那么一枚硬币投掷2次一定出现正面
,那么一枚硬币投掷2次一定出现正面
查看答案和解析>>
科目:高中数学 来源:2016届安徽蚌埠铁中高一下学期期中质量检测数学试卷(解析版) 题型:选择题
设△ABC的内角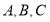 所对的边分别为
所对的边分别为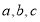 ,若
,若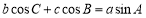 ,则
,则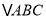 的形状为( )
的形状为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不确定
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一自主招生考试数学试卷(解析版) 题型:填空题
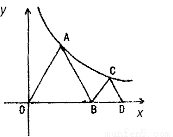
如图,点A、C都在函数 的图象上,点B、D都在
的图象上,点B、D都在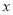 轴上,且使得△OAB、△BCD都是等边三角形,则点D的坐标为 .
轴上,且使得△OAB、△BCD都是等边三角形,则点D的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com