
设数列 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和,
项和, 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
(1) 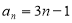 ,
,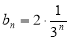 ;(2)m的最小值是
;(2)m的最小值是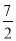 .
.
【解析】
试题分析:(1)确定数列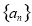 为的公差
为的公差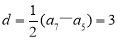 ,
,  ,即得
,即得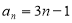 ,
,
由已知得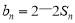 ,当
,当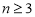 时,得
时,得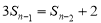 ,
,
两式相减整理得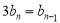 ,所以
,所以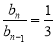
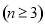 又
又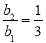 ,得知
,得知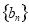 是以
是以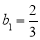 为首项,
为首项,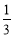 为公比的等比数列.
为公比的等比数列.
(2)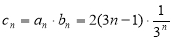
利用“错位相减法” 求和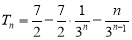 ,
,
从而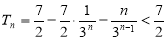
为使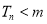 对
对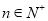 恒成立,得到
恒成立,得到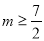 ,确定m的最小值是
,确定m的最小值是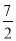 .
.
解得本题的关键是确定数列的基本特征.
(1) 数列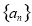 为等差数列,公差
为等差数列,公差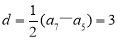 ,易得
,易得 ,
,
所以 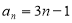 1分
1分
由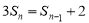 ,得
,得 ,即
,即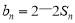 ,
,
所以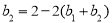 ,又
,又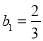 ,所以
,所以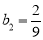 ,
,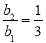 2分
2分
由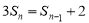 , 当
, 当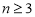 时,得
时,得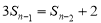 ,
,
两式相减得: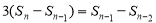 ,即
,即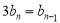 ,所以
,所以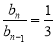
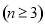 4分
4分
又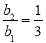 ,所以
,所以 是以
是以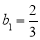 为首项,
为首项,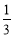 为公比的等比数列,于是
为公比的等比数列,于是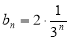 5分
5分
(2)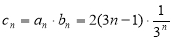
∴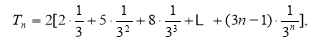 6分
6分
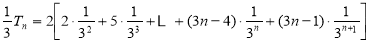 8分
8分
两式相减得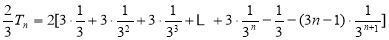 9分
9分
所以 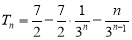 11分
11分
从而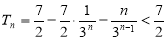
∵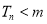 对
对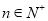 恒成立,∴
恒成立,∴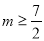 ∴m的最小值是
∴m的最小值是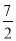 12分
12分
考点:等差数列、等比数列的通项公式及其求和公式,“错位相减法”.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2013-2014学年山东省日照市高三3月第一次模拟考试理科数学试卷(解析版) 题型:解答题
寒假期间,我市某校学生会组织部分同学,用“10分制”随机调查“阳光花园”社区人们的幸福度,现从调查人群中随机抽取16名,如果所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶);若幸福度分数不低于8.5分,则该人的幸福度为“幸福”.
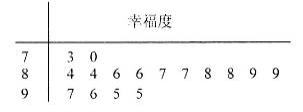
(1)求从这16人中随机选取3人,至少有2人为“幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记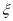 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求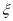 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
若函数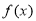 满足
满足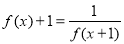 ,当x∈[0,1]时,
,当x∈[0,1]时,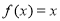 ,若在区间(-1,1]上,
,若在区间(-1,1]上, 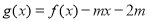 有两个零点,则实数m的取值范围是
有两个零点,则实数m的取值范围是
A.0<m≤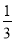 B.0<m<
B.0<m<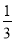 C.
C.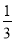 <m≤l D.
<m≤l D.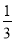 <m<1
<m<1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
下列命题错误的是
A.命题“若 ,则
,则 ”的逆否命题为“若x≠1,则
”的逆否命题为“若x≠1,则 ”
”
B.“x>2”是“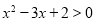 ”的充分不必要条件
”的充分不必要条件
C.对于命题p: R,使得
R,使得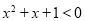 ,则
,则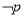 为:
为: R,均有
R,均有
D.若 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:填空题
已知直角梯形ABCD,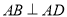 ,
,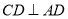 ,
,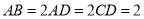 ,沿
,沿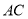 折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .
折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
函数 的部分图像如图所示,则
的部分图像如图所示,则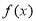 的解析式可以是( )
的解析式可以是( )

A. B.
B.
C.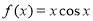 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:填空题
某公司一年购买某种货物400吨,每次都购买 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为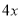 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则 ___ ____ 吨.
___ ____ 吨.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com