
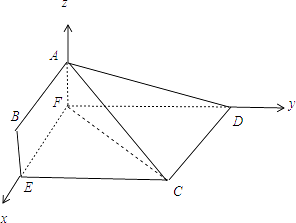
【题目】如图,四边形ABCD中,AB⊥CD,AD∥BC,AD=3,BC=2AB=2,E,F分别在BC,AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
(Ⅰ)若BE= ![]() ,在折叠后的线段AD上是否存在一点P,且
,在折叠后的线段AD上是否存在一点P,且 ![]() ,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
(Ⅱ)求三棱锥A﹣CDF的体积的最大值,并求此时二面角E﹣AC﹣F的余弦值.
【答案】解:(Ⅰ)∵平面ABEF⊥平面EFDC,平面ABEF∩平面EFDC=EF,
FD⊥EF,
∴FD⊥平面ABEF,又AF平面ABEF,
∴FD⊥AF,
在折起过程中,AF⊥EF,同时FD∩EF=F,
∴AF⊥平面EFDC,
以F为坐标原点,分别以FE,FD,FA所在直线为x,y,z轴,建立空间直角坐标系,
当BE= ![]() 时,F(0,0,0),A(0,0,
时,F(0,0,0),A(0,0, ![]() ),D(0,
),D(0, ![]() ,0),C(1,
,0),C(1, ![]() ,0),
,0),
平面ABEF的法向量 ![]() =(0,
=(0, ![]() ,0),
,0),
∵ ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() +
+ ![]() =
= ![]() ,
,
∴P(0, ![]() ,
, ![]() ),
),
∴ ![]() =(﹣1,
=(﹣1, ![]() ,
, ![]() ),
),
∵CP∥平面ABEF,∴ ![]() =
= ![]() =0,
=0,
解得 ![]() ,
,
∴线段AD上点P(0, ![]() ),且
),且 ![]() ,使得CP∥平面ABEF.
,使得CP∥平面ABEF.
(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,
∴VA﹣CDF= ![]() =
= ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,VA﹣CDF有最大值,且最大值为
时,VA﹣CDF有最大值,且最大值为 ![]() ,
,
∴A(0,0, ![]() ),C(1,
),C(1, ![]() ,0),D(0,
,0),D(0, ![]() ,0),E(1,0,0),
,0),E(1,0,0),
∴ ![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
), ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() ),
), ![]() =(0,0,
=(0,0, ![]() ),
), ![]() =(1,
=(1, ![]() ,0),
,0),
设平面AEC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 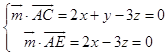 ,取x=3,得
,取x=3,得 ![]() =(3,0,2),
=(3,0,2),
设平面ACF的一个法向量 ![]() =(a,b,c),
=(a,b,c),
则 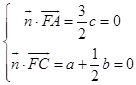 ,取a=1,得
,取a=1,得 ![]() =(1,﹣2,0),
=(1,﹣2,0),
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴二面角E﹣AC﹣F的余弦值为 ![]() .
.
【解析】(Ⅰ)推导出FD⊥EF,FD⊥AF,以F为坐标原点,分别以FE,FD,FA所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出线段AD上存在点P(0, ![]() ),
), ![]() ,使得CP∥平面ABEF.(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,推导出当x=
,使得CP∥平面ABEF.(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,推导出当x= ![]() 时,VA﹣CDF有最大值,且最大值为
时,VA﹣CDF有最大值,且最大值为 ![]() ,求出此时平面AEC的一个法向量和平面ACF的一个法向量,利用向量法能求出二面角E﹣AC﹣F的余弦值.
,求出此时平面AEC的一个法向量和平面ACF的一个法向量,利用向量法能求出二面角E﹣AC﹣F的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx(ω>0),将y=f(x)的图象向右平移 ![]() 个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
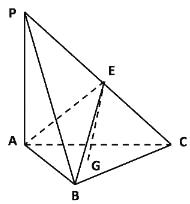
【题目】如图,在三棱锥P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB=BC=CA=AP=2,G是△ABC重心,E是线段PC上一点,且CE=λCP.
(1)当EG∥平面PAB时,求λ的值;
(2)当直线CP与平面ABE所成角的正弦值为![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是函数y=Asin(ωx+φ)(x∈R)在区间 ![]() 上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 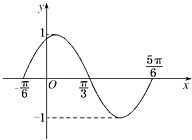
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)给出定义:
设f′(x)是函数y=f(x)的导数,f″(x)是函数f′(x)的导数,若方程f″(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.
某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数 ![]() ,请你根据上面探究结果,计算
,请你根据上面探究结果,计算![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ![]() ,∠CDA=120°,点N在线段PB上,且PN=2.
,∠CDA=120°,点N在线段PB上,且PN=2. 
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.

(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com