练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若实数x，y满足不等式组
    3x-y≤3
    x+y≥1
    x-y≥-1
    ，则z=2x+3y的最大值是（　　）
    A、13B、12C、11D、10
    考点：简单线性规划
    专题：不等式的解法及应用
    分析：作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．
    解答： 解：作出不等式对应的平面区域（阴影部分），
    由z=2x+3y，得y=-
    2
    3
    x+
    z
    3
    ，
    平移直线y=-
    2
    3
    x+
    z
    3
    ，由图象可知当直线y=-
    2
    3
    x+
    z
    3
    经过点A时，直线y=-
    2
    3
    x+
    z
    3
    的截距最大，此时z最大．
    由
    3x-y=3
    x-y=-1
    ，解得
    x=2
    y=3
    ，
    即A（2，3）．
    此时z的最大值为z=2×2+3×3=13，
    故选：A．
    点评：本题主要考查线性规划的应用，利用z的几何意义，通过数形结合是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    任意画一个正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了3个正方形，如图所示．若向图形中随机投一点，则所投点落在第三个正方形的概率是（　　）
    A、
    		2
    2
    B、
    1
    4
    C、
    1
    8
    D、
    1
    16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设不等式组
    x≤3
    y≤5
    4x+3y≥15
    所表示的平面区域为D．若圆C落在区域D中，则圆C的半径r的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    [x]表示不超过x的最大整数，已知f（x）=
    [x]
    x
    -a，当x＞0时，f（x）=
    [x]
    x
    -a有且仅有三个零点，则a的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面说法正确的是（　　）
    A、不存在既不是奇函数，有又不是偶函数的幂函数
    B、图象不经过点（-1，1）的幂函数一定不是偶函数
    C、如果两个幂函数的图象有三个公共点，那么这两个幂函数相同
    D、如果一个幂函数的图象不与y轴相交，则y=xα中α＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

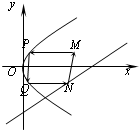    如图，从点M（x0，4）发出的光线，沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P，经抛物线反射后，穿过焦点射向抛物线上的点Q，再经抛物线反射后射向直线l：x-y-10=0上的点N，经直线反射后又回到点M，则x0等于（　　）
    A、5B、6C、7D、8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设全集U=R，M={x|
    1
    8
    ＜2x＜1}，N={x|ln（-x）＞0}，则M∩∁UN=（　　）
    A、{x|x≥-1}
    B、{x|-3＜x＜0}
    C、{x|x≤-3}
    D、{x|-1≤x＜0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的两个焦点分别为F1，F2，离心率为
    		2
    2
    ，且过点(2，
    		2
    )    ．
    （1）求椭圆C的标准方程；
    （2）过点F1作直线l1与椭圆交于M，N两点，过点F2作直线l2与椭圆交于P，Q两点，且直线l1，l2互相垂直，试问
    1
    |MN|
    +
    1
    |PQ|
    是否为定值？如果是，求出该定值；如果不是，求出其取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

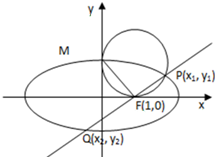    椭圆G：
    x2
    a2
    +
    y2
    b2
    =1    （a＞0，b＞0 ）与x轴交于A、B两点，F是它的右焦点，若
    FA
    •
    FB
    =-1且|OF|=1
    （1）求椭圆C的标准方程；
    （2）设椭圆G的上顶点为M，是否存在直线L，L交椭圆于P（x1，y1）、Q（x2，y2）两点，满足PQ⊥MF，且|PQ|=
    4
    3
    ，若存在，求直线L的方程，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案