Question

14．已知在△ABC中，∠C=90°，∠B=60°，设过点C在∠BCA内随机的作射线CM交斜边AB于点M，∠BCM＜30°的概率为P₁；在斜边AB上随机的取一点N，∠BCN＜30°的概率P₂，则 P₁＞P₂（填“＞”或“＜”或“=”）．

Answer 1

分析 根据题意，求出过点C在∠BCA内随机的作射线CM交斜边AB于点M，∠BCM＜30°的概率为P₁与在斜边AB上随机的取一点N，∠BCN＜30°的概率P₂，比较大小即可．

解答 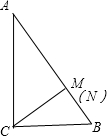解：如图所示，
△ABC中，∠C=90°，∠B=60°，
过点C在∠BCA内随机的作射线CM交斜边AB于点M，∠BCM＜30°的概率为P₁；
则P₁=$\frac{30°}{90°}$=$\frac{1}{3}$；
在斜边AB上随机的取一点N，∠BCN＜30°的概率P₂，
则P₂=$\frac{BN}{BA}$=$\frac{1}{4}$；
∴P₁＞P₂．
故答案为：＞．

点评 本题考查了几何概型的计算与应用问题，解题时应画出图形，结合图形来解答，是基础题目．