
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
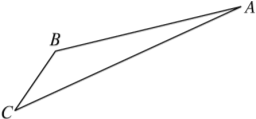
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
【答案】(1)1 040 m;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)在![]() 中,因为cos A=
中,因为cos A=![]() ,cos C=
,cos C=![]() ,所以sin A=
,所以sin A=![]() ,sin C=
,sin C=![]() .
.
从而sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=![]() .
.
由正弦定理![]() ,可得
,可得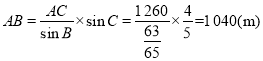 .
.
所以索道AB的长为1 040 m.(3分)
(2)假设乙出发t 分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,
所以由余弦定理,得![]() ,
,
因为![]() ,即0≤t≤8,所以当
,即0≤t≤8,所以当![]() 分钟时,甲、乙两游客距离最短.(6分)
分钟时,甲、乙两游客距离最短.(6分)
(3)由正弦定理![]() ,得
,得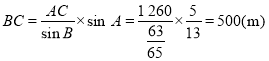 .
.
乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.
设乙步行的速度为v m/min,由题意得![]() ,解得
,解得![]() ,
,
所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在![]() (单位:m/min)范围内.(10分)
(单位:m/min)范围内.(10分)


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣|x2﹣ax﹣2|,a为实数.
(1)当a=1时,求函数f(x)在[0,3]上的最小值和最大值;
(2)若函数f(x)在(﹣∞,﹣1)和(2,+∞)上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对一切实数x,y都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值;
(2)求f(x)的解析式;
(3)若g(x)=kx﹣2k+5,对任意的m∈[1,4],总存在n∈[1,4],使得f(m)=g(n)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省数学学业水平考试成绩分为A、B、C、D四个等级,在学业水平成绩公布后,从该省某地区考生中随机抽取60名考生,统计他们的数学成绩,部分数据如下:
等级 | A | B | C | D |
频数 | 24 | 12 | ||
频率 | 0.1 |
(1)补充完成上述表格中的数据;
(2)现按上述四个等级,用分层抽样的方法从这60名考生中抽取10名,在这10名考生中,从成绩A等和B等的所有考生中随机抽取2名,求至少有一名成绩为A等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() (a>0,b>0)过点A(1,0),且离心率为
(a>0,b>0)过点A(1,0),且离心率为 ![]()
(1)求双曲线C的方程;
(2)已知直线x﹣y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知z为复数,ω=z+ ![]() 为实数,
为实数,
(1)当﹣2<ω<10,求点Z的轨迹方程;
(2)当﹣4<ω<2时,若u= ![]() (α>0)为纯虚数,求:α的值和|u|的取值范围.
(α>0)为纯虚数,求:α的值和|u|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com