已知函数f(x)的定义域为R.若?常数c>0,对?x∈R,有f(x+c)>f(x-c),则称函数f(x)具有性质P.给定下列三个函数:
①f(x)=2x; ②f(x)=sinx; ③f(x)=x3-x.
其中,具有性质P的函数的序号是 .
【答案】
分析:根据f(x)=2
x 是R上的增函数,故满足条件.因为f(x)=sinx是周期函数,故不满足条件.对于f(x)=x
3-x,利用导数求得函数的减区间为(-
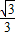
,
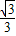
)内递减,要想满足f(x+c)>f(x-c),只须c>
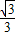
就可以了,故满足条件,从而得出结论.
解答:解:①因为f(x)=2
x 是R上的增函数,所以满足f(x+c)>f(x-c),故此函数f(x)具有性质P.
②因为f(x)=sinx的最小正周期为2π,不是在R上的增函数,所以不满足f(x+c)>f(x-c),故此函数f(x)
具有性质P.
③∵f(x)=x
3-x,∴f′(x)=3x
2-1,当f′(x)>0时,函数f(x)是增函数,f′(x)<0时,函数f(x)
是递减函数.
即在(-
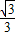
,
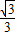
)内递减,要想满足f(x+c)>f(x-c),只须c>
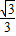
就可以了,如c=1就满足了.
所以,满足f(x+c)>f(x-c).
故答案为 ①③.
点评:本题主要考查新定义,命题真假的判断,函数的周期性和单调性的应用,属于基础题.

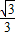 ,
,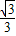 )内递减,要想满足f(x+c)>f(x-c),只须c>
)内递减,要想满足f(x+c)>f(x-c),只须c>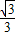 就可以了,故满足条件,从而得出结论.
就可以了,故满足条件,从而得出结论.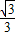 ,
,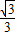 )内递减,要想满足f(x+c)>f(x-c),只须c>
)内递减,要想满足f(x+c)>f(x-c),只须c>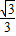 就可以了,如c=1就满足了.
就可以了,如c=1就满足了.

 应用题作业本系列答案
应用题作业本系列答案