
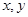 都是正数,
都是正数,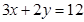 ,求
,求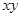 的最大值
的最大值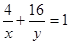 ,求
,求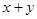 的最小值.
的最小值. ,
, 的最大值随之而定;(2)如果直接利用基本不等式则有
的最大值随之而定;(2)如果直接利用基本不等式则有 ①,
①, ,因此
,因此 ②,这样就可能得出
②,这样就可能得出 的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是
的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是 ,
, ,不等式②取等号的条件是
,不等式②取等号的条件是 ,即不等式①②不能同时取等号,故
,即不等式①②不能同时取等号,故 的最小值不是32.正确的解法是把
的最小值不是32.正确的解法是把 看作
看作 ,把其中的1用已知
,把其中的1用已知 代换,即
代换,即 ,展开后就可以直接利用基本不等式求出结果.
,展开后就可以直接利用基本不等式求出结果. ·3x·2y≤
·3x·2y≤
 2=6 4分
2=6 4分 即
即 时取“=”号.
时取“=”号. 且
且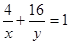 得
得

 , 10分
, 10分 ,即x=12且y=24时,等号成立,
,即x=12且y=24时,等号成立,

 精英口算卡系列答案
精英口算卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com