练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，已知点，，动点不在轴上，直线、的斜率之积．

    （Ⅰ）求动点的轨迹方程；

    （Ⅱ）经过点的两直线与动点的轨迹分别相交于、两点。是否存在常数，使得任意满足的直线恒过线段的中点？请说明理由．

    【答案】(1)（）(2)见解析

    【解析】【试题分析】(I)（）,将已知代入化简的的轨迹方程.(2)猜想时，直线恒过线段的中点.设出直线的方程,代入椭圆方程求得点坐标,同理写出直线的方程,代入椭圆方程得到点的坐标.由此证得直线恒过线段的中点.

    【试题解析】

    （Ⅰ）设（），则，，

    由得，，

    化简整理得，动点的轨迹方程为（）

    （Ⅱ）动点的轨迹与轴的两个交点为、，

    猜想时，直线恒过线段的中点

    记，则直线：，

    解得

    当时，，则直线：，

    同理可得

    线段的中点是线段的中点，所以直线恒过线段的中点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，离心率为，右焦点到直线的距离为2.

    （1）求椭圆的方程；

    （2）椭圆下顶点为，直线（）与椭圆相交于不同的两点，当时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图2，在三棱锥A-BCD中，AB=CD=4, AC=BC=AD=BD=3.

    (I)证明:ABCD;

    (II) E在线段BC上，BE=2EC, F是线段AC的中点，求平面ADE与平面BFD所成锐二面角的余弦值

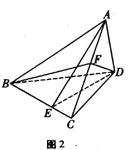
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等差数列中，已知公差， ，且， ， 成等比数列.

    （1）求数列的通项公式；

    （2）求.

    【答案】（1）；（2）100

    【解析】试题分析：（1）根据题意， ， 成等比数列得得求出d即可得通项公式；（2）求项的绝对前n项和，首先分清数列有多少项正数项和负数项，然后正数项绝对值数值不变，负数项绝对值要变号，从而得，得，由，得，∴ 计算 即可得出结论

    解析：（1）由题意可得，则， ，

    ，即，

    化简得，解得或（舍去）.

    ∴.

    （2）由（1）得时，

    由，得，由，得，

    ∴

    .

    ∴.

    点睛：对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决，对于第二问前n项的绝对值的和问题，首先要找到数列由多少正数项和负数项，进而找到绝对值所影响的项，然后在求解即可得结论

    【题型】解答题
    【结束】
    18

    【题目】甲、乙两家销售公司拟各招聘一名产品推销员，日工资方案如下: 甲公司规定底薪80元，每销售一件产品提成1元; 乙公司规定底薪120元，日销售量不超过45件没有提成，超过45件的部分每件提成8元.

    (I)请将两家公司各一名推销员的日工资 (单位: 元) 分别表示为日销售件数的函数关系式;

    (II)从两家公司各随机选取一名推销员，对他们过去100天的销售情况进行统计，得到如下条形图。若记甲公司该推销员的日工资为,乙公司该推销员的日工资为 (单位: 元)，将该频率视为概率，请回答下面问题:

    某大学毕业生拟到两家公司中的一家应聘推销员工作，如果仅从日均收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某石化集团获得了某地深海油田区块的开采权．集团在该地区随机初步勘探了部分几口井．取得了地质资料，进入全面勘探时期后．集团按网络点来布置井位进行全面勘探．由于勘探一口井的费用很高．如果新设计的井位与原有井位重合或接近．便利用旧并的地质资料．不必打这日新并，以节约勘探费与用，勘探初期数据资料见如表：

    井号

    坐标

    钻探深度

    出油量

    （参考公式和计算结果：，，，）．

    （）号旧井位置线性分布，借助前组数据求得回归直线方程为，求的值．

    （）现准备勘探新井，若通过，，，号井计算出的，的值（，精确到）相比于（）中的，，值之差不超过．则使用位置最接近的已有旧井．否则在新位置打开，请判断可否使用旧井？

    （）设出油量与勘探深度的比值不低于的勘探井称为优质井，那么在原有口井中任意勘探口井，求勘探优质井数的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，是常数．

    （Ⅰ）求曲线在点处的切线方程，并证明对任意，切线经过定点；

    （Ⅱ）证明：时，有两个零点、，且．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E:=1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=-x+3与椭圆E有且只有一个公共点T.

    (1)求椭圆E的方程及点T的坐标;

    (2)设O是坐标原点,直线l'平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P,证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数，关于的不等式的解集为，，设．

    （）求的值．

    （）如何取值时，函数存在极值点，并求出极值点．

    （）若，且，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：

    记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用（单位：元）, 表示购机的同时购买的易损零件数.

    （Ⅰ）若=19,求y与x的函数解析式；

    （Ⅱ）若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值；

    （Ⅲ）假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件？

    查看答案和解析>>

    同步练习册答案