
分析 可取PQ的中点D,并连接CD,CP,CQ,OC,从而得到CD⊥PQ,根据向量加法的几何意义,向量加法的平行四边形法则,以及向量数量积的运算便可得出$\overrightarrow{OP}•\overrightarrow{OQ}={\overrightarrow{OC}}^{2}+2\overrightarrow{OC}•\overrightarrow{CD}+\overrightarrow{CP}•\overrightarrow{CQ}$,而$\overrightarrow{CP}=\overrightarrow{CD}+\overrightarrow{DP},\overrightarrow{CQ}=\overrightarrow{CD}-\overrightarrow{DP}$,从而进行数量积的运算即可求出$\overrightarrow{CP}•\overrightarrow{CQ}={\overrightarrow{CD}}^{2}-{\overrightarrow{DP}}^{2}$,带入前面的式子即可求出$\overrightarrow{OP}•\overrightarrow{OQ}$的值.
解答 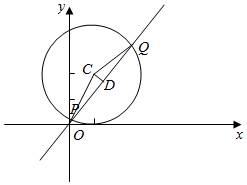 解:如图,
解:如图,
取PQ中点D,连接CD,CP,CQ,OC,则CD⊥PQ;
∴$\overrightarrow{OP}•\overrightarrow{OQ}=(\overrightarrow{OC}+\overrightarrow{CP})•(\overrightarrow{OC}+\overrightarrow{CQ})$
=${\overrightarrow{OC}}^{2}+\overrightarrow{OC}•(\overrightarrow{CP}+\overrightarrow{CQ})+\overrightarrow{CP}•\overrightarrow{CQ}$
=${\overrightarrow{OC}}^{2}+2\overrightarrow{OC}•\overrightarrow{CD}+(\overrightarrow{CD}+\overrightarrow{DP})$$•(\overrightarrow{CD}-\overrightarrow{DP})$
=${\overrightarrow{OC}}^{2}+2(\overrightarrow{OD}+\overrightarrow{DC})•\overrightarrow{CD}$$+{\overrightarrow{CD}}^{2}-{\overrightarrow{DP}}^{2}$
=${\overrightarrow{OC}}^{2}-2{\overrightarrow{CD}}^{2}+{\overrightarrow{CD}}^{2}-{\overrightarrow{DP}}^{2}$
=${\overrightarrow{OC}}^{2}-({\overrightarrow{CD}}^{2}+{\overrightarrow{DP}}^{2})$
=${\overrightarrow{OC}}^{2}-{\overrightarrow{CP}}^{2}$
=5-4
=1.
故答案为:1.
点评 考查向量加法、数乘的几何意义,向量加法的平行四边形法则,以及向量数量积的运算及计算公式,向量数量积的坐标运算.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{an}的项随n的增大而增大 | |
| B. | 数列{an}的项随n的增大而减少 | |
| C. | 对于数列{an}中的项an,存在唯一k(k∈N*),使an≤ak对任意n∈N*都成立 | |
| D. | 数列{an}中存在相等的两个项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 点击次数(x万次) | 0≤x<50 | 50≤x<100 | 100≤x<150 | x≥150 |
| 等级 | 差 | 中 | 良 | 优 |
| 点击次数(x万次) | 0≤x<50 | 50≤x<100 | 100≤x<150 | x≥150 |
| 天数 | 5 | 11 | 10 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com