
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.
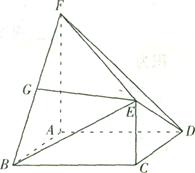
(1)求证:EG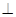 面ABF;
面ABF;
(2)若AF=AB,求二面角B—EF—D的余弦值.
(1)∵在正三角形ABC中,CM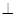 AB,又AF
AB,又AF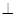 CM∴EG
CM∴EG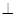 AB, EG
AB, EG AF,∴EG
AF,∴EG 面ABF.
面ABF.
(2)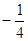
【解析】
试题分析:(1)取AB的中点M,连结GM,MC,G为BF的中点,
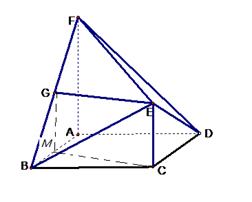
所以GM //FA,又EC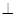 面ABCD, FA
面ABCD, FA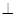 面ABCD,
面ABCD,
∵CE//AF,
∴CE//GM,
∵面CEGM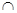 面ABCD=CM,
面ABCD=CM,
EG// 面ABCD,
∴EG//CM,
∵在正三角形ABC中,CM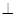 AB,又AF
AB,又AF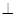 CM
CM
∴EG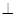 AB, EG
AB, EG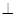 AF,
AF,
∴EG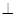 面ABF.
面ABF.
(2)建立如图所示的坐标系,设AB=2,
则B(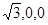 )E(0,1,1) F(0,-1,2)
)E(0,1,1) F(0,-1,2)
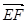 =(0,-2,1) ,
=(0,-2,1) , 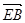 =(
=(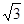 ,-1,-1),
,-1,-1), 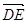 =(
=(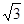 ,1, 1),
,1, 1),
设平面BEF的法向量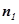 =(
=(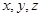 )则
)则
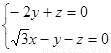 令
令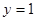 ,则
,则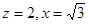 ,
,
∴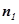 =(
=(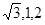 )
)
同理,可求平面DEF的法向量 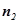 =(-
=(-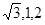 )
)
设所求二面角的平面角为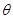 ,则
,则
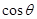 =
=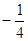 .
.
考点:用空间向量求平面间的夹角;直线与平面垂直的判定;二面角的平面角及求法.
点评:本题考查线面垂直,考查面面角,正确运用线面垂直的判定,求出平面的法向量是解题的关键.


科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)已知数列{an}中,a1=1,a2=3且2an+1=an+2+an(n∈N*).数列{bn}的前n项和为Sn,其中b1=- ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)若Tn= +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)已知椭圆的的右顶点为A,离心率 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段 为直径的圆经过焦点
为直径的圆经过焦点 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年贵州省高三年级第五次月考文科数学 题型:解答题
(本小题满分l2分)(注意:在试题卷上作答无效)
求经过A(2,-1),和直线x+y=1相切,且圆心在直线y=-2x上的圆的方程
(I)求出圆的标准方程
(II)求出(I)中的圆与直线3x+4y=0相交的弦长AB
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三上学期10月月考理科数学卷 题型:解答题
(本小题满分l2分)设命题 :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 或
或 ”是假命题,求实数
”是假命题,求实数 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com