
分析 (1)根据绝对值不等式|a+b|≥|a-b|便可得出|x+3|+|x-1|≥4,从而得出f(x)的最小值为4,即得到t=4;
(2)可知a+b=4,a>0,b>0,从而有$1=\frac{a+b}{4}$,这样便可得出$\frac{1}{a}+\frac{4}{b}=\frac{b}{4a}+\frac{a}{b}+\frac{5}{4}$,而根据基本不等式即可得出$\frac{b}{4a}+\frac{a}{b}≥1$,这样便可证出$\frac{1}{a}+\frac{4}{b}≥\frac{9}{4}$.
解答 解:(1)f(x)=|x+3|+|x-1|≥|(x+3)-(x-1)|=4;
∴f(x)的最小值为4;
∴t=4;
(2)证明:a>0,b>0,a+b=4;
∴$1=\frac{a+b}{4},4=a+b$;
∴$\frac{1}{a}+\frac{4}{b}=\frac{a+b}{4a}+\frac{a+b}{b}$
=$\frac{b}{4a}+\frac{a}{b}+\frac{5}{4}$
$≥2\sqrt{\frac{b}{4a}•\frac{a}{b}}+\frac{5}{4}=\frac{9}{4}$,当且仅当$\frac{b}{4a}=\frac{a}{b}$,即b=$2a=\frac{8}{3}$时取“=”;
即$\frac{1}{a}+\frac{4}{b}≥\frac{9}{4}$.
点评 考查绝对值不等式公式:|a|+|b|≥|a-b|,以及基本不等式的应用,应用基本不等式要注意判断等号能否取到.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
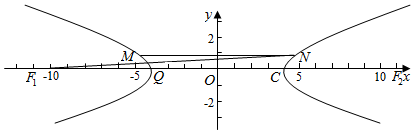
| A. | y=$±\sqrt{2}$x | B. | y=$±\sqrt{3}$x | C. | y=±2x | D. | y=$±\sqrt{5}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com