
【题目】设函数![]() ,
,
(1)求函数![]() 在
在![]() 上的值域
上的值域
(2)设![]() ,若方程
,若方程![]() 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)对函数进行求导得![]() ,再根据导数不等式求得单调区间和极值,并与区间端点函数值比较,从而得到函数在闭区间的最值,从而得到函数的值域;
,再根据导数不等式求得单调区间和极值,并与区间端点函数值比较,从而得到函数在闭区间的最值,从而得到函数的值域;
(2)由![]() 知:
知:![]() ,显然
,显然![]() 是其一个根,所以方程
是其一个根,所以方程![]() 有两个不相等的实数根等价于方程
有两个不相等的实数根等价于方程![]() 有且仅有一个根且不为0,再利用导数研究
有且仅有一个根且不为0,再利用导数研究![]() 的最值和单调性,从而得到参数的取值范围.
的最值和单调性,从而得到参数的取值范围.
(1)![]() ,令
,令![]() ,则
,则![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递增
上递增
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递减
上递减
因为![]() ,
,
所以函数![]() 的最小值为
的最小值为![]() ,最大值为0,
,最大值为0,
所以函数![]() 的值域是
的值域是![]() .
.
(2)由![]() 知:
知:![]() ,显然
,显然![]() 是其一个根,所以方程
是其一个根,所以方程![]() 有两个不相等的实数根等价于方程
有两个不相等的实数根等价于方程![]() 有且仅有一个根且不为0;
有且仅有一个根且不为0;
令![]() .
.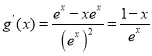 ,
,
易知![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
当![]() 时,
时,![]() ,且
,且![]() ,
,
若方程![]() 有且仅有一个根且不为0,
有且仅有一个根且不为0,
所以![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线 (
(![]() 为参数),
为参数),![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(I)写出曲线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(II)在极坐标系中,已知射线![]() 分别与曲线
分别与曲线![]() 及圆
及圆![]() 相交于
相交于![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目:高中数学 来源: 题型:
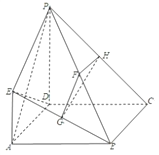
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆的四个顶点构成的四边形面积为
,椭圆的四个顶点构成的四边形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆上的一点,过
是椭圆上的一点,过![]() 且斜率等于
且斜率等于![]() 的直线与椭圆
的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .求
.求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月25日,第![]() 届罗马尼亚数学大师赛(简称
届罗马尼亚数学大师赛(简称![]() )于罗马尼亚首都布加勒斯特闭幕,最终成绩揭晓,以色列选手排名第一,而中国队无一人获得金牌,最好成绩是获得银牌的第
)于罗马尼亚首都布加勒斯特闭幕,最终成绩揭晓,以色列选手排名第一,而中国队无一人获得金牌,最好成绩是获得银牌的第![]() 名,总成绩排名第
名,总成绩排名第![]() .而在分量极重的国际数学奥林匹克(
.而在分量极重的国际数学奥林匹克(![]() )比赛中,过去拿冠军拿到手软的中国队,也已经有连续
)比赛中,过去拿冠军拿到手软的中国队,也已经有连续![]() 年没有拿到冠军了.人们不禁要问“中国奥数究竟怎么了?”,一时间关于各级教育主管部门是否应该下达“禁奥令”成为社会热点.某重点高中培优班共
年没有拿到冠军了.人们不禁要问“中国奥数究竟怎么了?”,一时间关于各级教育主管部门是否应该下达“禁奥令”成为社会热点.某重点高中培优班共![]() 人,现就这
人,现就这![]() 人“禁奥令”的态度进行问卷调查,得到如下的列联表:
人“禁奥令”的态度进行问卷调查,得到如下的列联表:
不应下“禁奥令” | 应下“禁奥令” | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
若采用分层抽样的方法从![]() 人中抽出
人中抽出![]() 人进行重点调查,知道其中认为不应下“禁奥令”的同学共有
人进行重点调查,知道其中认为不应下“禁奥令”的同学共有![]() 人.
人.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为对下“禁奥令”的态度与性别有关?请说明你的理由;
的把握认为对下“禁奥令”的态度与性别有关?请说明你的理由;
(2)现从这![]() 人中抽出
人中抽出![]() 名男生、
名男生、![]() 名女生,记此
名女生,记此![]() 人中认为不应下“禁奥令”的人数为
人中认为不应下“禁奥令”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式与数据:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的准线为
的准线为![]() ,其焦点为F,点B是抛物线C上横坐标为
,其焦点为F,点B是抛物线C上横坐标为![]() 的一点,若点B到
的一点,若点B到![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线C的方程,
(2)设A是抛物线C上异于顶点的一点,直线AO交直线![]() 于点M,抛物线C在点A处的切线m交直线
于点M,抛物线C在点A处的切线m交直线![]() 于点N,求证:以点N为圆心,以
于点N,求证:以点N为圆心,以![]() 为半径的圆经过
为半径的圆经过![]() 轴上的两个定点.
轴上的两个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com