
【题目】已知数列{an}的前n项和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() +(﹣1)nan , 求数列{bn}的前2n项和.
+(﹣1)nan , 求数列{bn}的前2n项和.
【答案】解:(Ⅰ)当n=1时,a1=s1=1,当n≥2时,an=sn﹣sn﹣1= ![]() ﹣
﹣ ![]() =n,
=n,
∴数列{an}的通项公式是an=n.
(Ⅱ)由(Ⅰ)知,bn=2n+(﹣1)nn,记数列{bn}的前2n项和为T2n , 则
T2n=(21+22+…+22n)+(﹣1+2﹣3+4﹣…+2n)
= ![]() +n=22n+1+n﹣2.
+n=22n+1+n﹣2.
∴数列{bn}的前2n项和为22n+1+n﹣2
【解析】(Ⅰ)利用公式法即可求得;(Ⅱ)利用数列分组求和即可得出结论.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系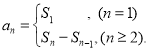 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数
为偶函数
(1)求实数a的值;
系;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判断λ与E的
,判断λ与E的
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
查看答案和解析>>
科目:高中数学 来源: 题型:
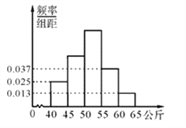
【题目】人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1组、第2组、第3组中用分层抽样的方法抽取6人进行测试.若从这6人中随机选取2人去共同完成某项任务,求这2人来自于同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式a|x|>x2﹣ ![]() 对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
A.( ![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
B.(0, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.( ![]() ,1)∪(1,2)
,1)∪(1,2)
D.(0, ![]() )∪(1,2)
)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点. 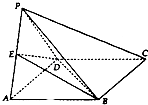
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
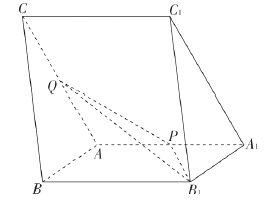
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(2cosx,1).
=(2cosx,1).
(1)若 ![]() ∥
∥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() ⊥
⊥ ![]() ,又x∈[π,2π],求sinx+cosx的值.
,又x∈[π,2π],求sinx+cosx的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com