
【题目】若不等式a|x|>x2﹣ ![]() 对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
A.( ![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
B.(0, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.( ![]() ,1)∪(1,2)
,1)∪(1,2)
D.(0, ![]() )∪(1,2)
)∪(1,2)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题。
(1)已知等比数列{an}中,a1=﹣1,a4=64,求q与S4
(2)已知等差数列{an}中,a1= ![]() ,d=﹣
,d=﹣ ![]() ,Sn=﹣15,求n及an .
,Sn=﹣15,求n及an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() +(﹣1)nan , 求数列{bn}的前2n项和.
+(﹣1)nan , 求数列{bn}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
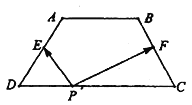
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com