
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 和
和![]() 是两个边长为2的正三角形,
是两个边长为2的正三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
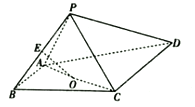
(1)证明:![]() 平面
平面![]() .
.
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)见解析;(2)当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,证明OE为三角形BPF的中位线,得
,证明OE为三角形BPF的中位线,得![]() 即可证明(2)证明
即可证明(2)证明![]() 平面
平面![]() ,由
,由![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() 的平行线,分别以它们作为
的平行线,分别以它们作为![]() 轴,以
轴,以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,求平面
轴建立如图所示的空间直角坐标系,求平面![]() 的法向量,假设线段
的法向量,假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,得
,得![]() ,由直线
,由直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 列
列![]() 的方程求解即可
的方程求解即可
(1)证明:设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 为正方形.
为正方形.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 为
为![]() ,
,![]() 的交点,
的交点,
∴![]() 为
为![]() 的中点,即OE为三角形BPF的中位线
的中点,即OE为三角形BPF的中位线
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又因为![]() ,所以过
,所以过![]() 分别作
分别作![]() ,
,![]() 的平行线,分别以它们作为
的平行线,分别以它们作为![]() 轴,
轴,
以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
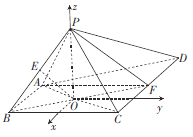
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
假设线段![]() 上存在一点
上存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
设![]() ,则
,则![]() ,
,
即![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则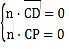 ,即
,即![]() .
.
取![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,令
,令![]() ,
,
得![]() ,
,
化简并整理得![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
所以,当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
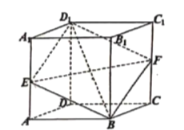
【题目】如图所示,直平行六面体![]() 的所有棱长都为2,
的所有棱长都为2,![]() ,过体对角线
,过体对角线![]() 的截面S与棱
的截面S与棱![]() 和
和![]() 分别交于点E、F,给出下列命题中:
分别交于点E、F,给出下列命题中:
①四边形![]() 的面积最小值为
的面积最小值为![]() ;
;
②直线EF与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
③四棱锥![]() 的体积为定值;
的体积为定值;
④点![]() 到截面S的距离的最小值为
到截面S的距离的最小值为![]() .
.
其中,所有真命题的序号为( )
A.①②③B.①③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车.每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车.今年初投入了电力型公交车120辆,混合动力型公交车300辆,计划以后电力型车每年的投入量比上一年增加![]() ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入![]() 辆.设
辆.设![]() ,
,![]() 分别为第
分别为第![]() 年投入的电力型公交车,混合动力型公交车的数量,设
年投入的电力型公交车,混合动力型公交车的数量,设![]() ,
,![]() 分别为
分别为![]() 年里投入的电力型公交车,混合动力型公交车的总数量.
年里投入的电力型公交车,混合动力型公交车的总数量.
(1)求![]() ,
,![]() ,并求
,并求![]() 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数![]() ;
;
(2)该市计划用8年的时间完成全部更换,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产能利用率是指实际产出与生产能力的比率,工r产能利用率是衡量工业生产经营状况的重要指标.下图为国家统计局发布的2015年至2018年第2季度我国工业产能利用率的折线图.
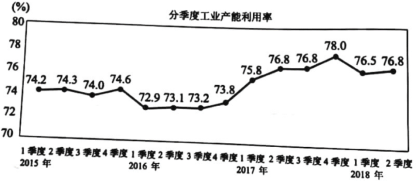
在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2016年第二季度与2015年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2015年第二季度与2015年第一季度相比较.
据上述信息,下列结论中正确的是( ).
A. 2015年第三季度环比有所提高B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高D. 2018年第一季度环比有所提高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是_____________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2,AB=1,E为AD中点,F为CC1中点.
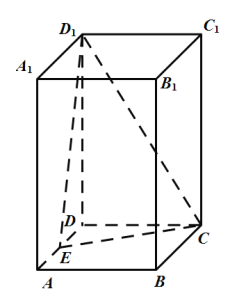
(1)求证:AD⊥D1F;
(2)求证:CE//平面AD1F;
(3)求AA1与平面AD1F成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商在销售某型号手机时开展“手机碎屏险”活动.用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费
元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例):
元时愿意购买该“手机碎屏险”的用户比例):

(1)根据上面的数据计算得![]() ,求出
,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若愿意购买该“手机碎屏险”的用户比例超过![]() ,则手机厂商可以获利,现从表格中的
,则手机厂商可以获利,现从表格中的![]() 种保费任取
种保费任取![]() 种,求这
种,求这![]() 种保费至少有一种能使厂商获利的概率.
种保费至少有一种能使厂商获利的概率.
附:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com