
【题目】在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2,AB=1,E为AD中点,F为CC1中点.
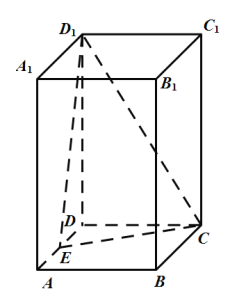
(1)求证:AD⊥D1F;
(2)求证:CE//平面AD1F;
(3)求AA1与平面AD1F成角的余弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
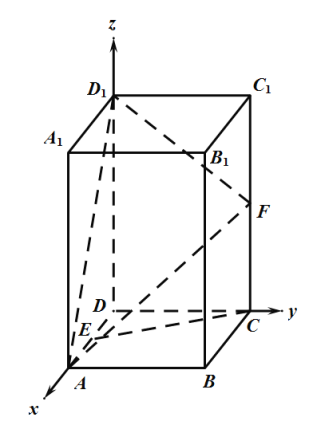
长方体中有垂直关系,因此以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,写出各点坐标,
(1)求出两条直线的方向向量,由向量垂直得直线垂直;
(2)求直线方向向量,平面的法向量,由方向向量与法向量垂直,证得线面平行;
(3)求直线方向向量,平面的法向量,由直线方向向量与平面法向量夹角的余弦值的绝对值等于线面角的正弦值,再计算余弦值.
(1)证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A(1,0,0),D(0,0,0),D1(0,0,2),F(0,1,1),
![]() =(-1,0,0),
=(-1,0,0),![]() =(0,1,-1),
=(0,1,-1),
![]() =0,
=0,
∴AD⊥D1F.
(2)证明:E(![]() ,0,0),C(0,1,0),A(1,0,0),
,0,0),C(0,1,0),A(1,0,0),
D1(0,0,2),F(0,1,1),
![]() =(
=(![]() ,-1,0),
,-1,0),![]() =(-1,0,2),
=(-1,0,2),![]() =(-1,1,1),
=(-1,1,1),
设平面AD1F的法向量![]() =(x,y,z),
=(x,y,z),
则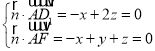 ,取z=1,得
,取z=1,得![]() =(2,1,1),
=(2,1,1),
∵![]() =
=![]() =0,CE平面AD1F,
=0,CE平面AD1F,
∴CE//平面AD1F.
(3)解:![]() =(0,0,2),平面AD1F的法向量
=(0,0,2),平面AD1F的法向量![]() =(2,1,1),
=(2,1,1),
设AA1与平面AD1F成角为θ,
则sinθ=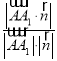 =
=![]() =
=![]() ,
,
cosθ=![]() =
=![]() .
.
∴AA1与平面AD1F成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() :
:![]() 经过伸缩变换
经过伸缩变换![]() ,后得到曲线
,后得到曲线![]() 以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为
以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为![]()
![]() 求曲线
求曲线![]() 的直角坐标方程及直线l的直角坐标方程;
的直角坐标方程及直线l的直角坐标方程;
![]() 在
在![]() 上求一点M,使点M到直线l的距离最小,并求出最小距离.
上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求![]() 的周长;
的周长;
(2)设点![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在第一象限,点
在第一象限,点![]() 在线段
在线段![]() 上.若
上.若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)设直线![]() 不平行于坐标轴,点
不平行于坐标轴,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .求
.求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
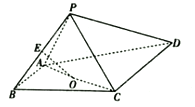
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 和
和![]() 是两个边长为2的正三角形,
是两个边长为2的正三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() .
.
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )

A. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
D. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,
,![]() 分别交直线
分别交直线![]() 于,
于,![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试问:
,试问:![]() 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三位同学毕业后,发现市内一些小家电配件的批发商每天的批发零售的生意很火爆,于是他们三人决定利用所学专业进行自主创业,专门生产这类小家电配件,并与经销商签订了经销合同,他们生产出的小家电配件,以每件![]() 元的价格全部由经销商包销.经市场调研,生产这类配件,每月需要投入固定成本为
元的价格全部由经销商包销.经市场调研,生产这类配件,每月需要投入固定成本为![]() 万元,每生产
万元,每生产![]() 万件配件,还需再投入资金
万件配件,还需再投入资金![]() 万元.在月产量不足
万元.在月产量不足![]() 万件时,
万件时,![]() (万元);在月产量不小于
(万元);在月产量不小于![]() 万件时,
万件时,![]() (万元).已知月产量是
(万元).已知月产量是![]() 万件时,需要再投入的资金是
万件时,需要再投入的资金是![]() 万元.
万元.
(1)试将生产这些小家电的月利润![]() (万元)表示成月产量
(万元)表示成月产量![]() (万件)的函数;(注:月利润
(万件)的函数;(注:月利润![]() 月销售收入
月销售收入![]() 固定成本
固定成本![]() 再投入成本)
再投入成本)
(2)月产量为多少万件时,这三位同学生产这些配件获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com