
已知点M(k,l),P(m,n)(klmn≠0)是曲线C上的两点,点M,N关于x轴对 称,直线MP,NP分别交x轴于点E(xE,0)和点F(xF,0).
称,直线MP,NP分别交x轴于点E(xE,0)和点F(xF,0).
(1)用k,l,m,n分别表示xE和xF;
(2)当曲线C的方程分别为:x2+y2=R2(R>0),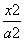 +
+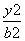 =1(a>b>0)时,探究xE·xF的值是否与点M,N,P的位置相关;
=1(a>b>0)时,探究xE·xF的值是否与点M,N,P的位置相关;
(3)类比(2)的探究过程,当曲线C的方程为y2=2px(p>0)时,探究xE与xF经加、减、乘、除的某一种运算后为定值的一个正确结论(只要求写出你的探究 结论,无须证明).
结论,无须证明).
解析:(1)依题意N(k,-l),且klmn≠0及MP,NP与x轴有交点知:
M,P,N为不同点,直线PM的方程为y= (x-m)+n,
(x-m)+n,
直线PN的方程为y=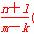 (x-m)+n,
(x-m)+n,
则xE=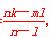 ,同理可得xF=
,同理可得xF=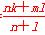 .
.
(2)∵M,P在圆C:x2+y2=R2上,
∴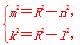 xE·xF=
xE·xF=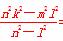 =
=
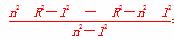 =R2(定值).
=R2(定值).
∴xE·xF的值与点M,N,P位置无关.
同理,∵M,P在椭圆C: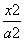 +
+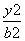 =1(a>b>0)上,
=1(a>b>0)上,
∴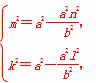 ∴xE·xF=
∴xE·xF=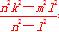 =
=
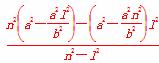 =a2(定值).
=a2(定值).
∴xE·xF的值与点M,N,P位置无关.
(3)一个探究结论是:xE+xF=0.
证明如下:依题意,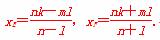
∵M,P在抛物线C:y2=2px(p>0)上,
∴n2=2pm,l2=2pk.
xE+xF=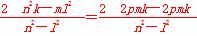 =0.
=0.
∴xE+xF为定值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
下列命题错误的是 ( )
A、命题“若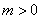 ,则方程
,则方程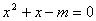 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程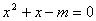 无实数根,则
无实数根,则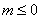 ”
”
B、“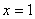 ”是“
”是“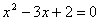 ”的充分不必要条件
”的充分不必要条件
C、对于命题 ,使得
,使得 ,则
,则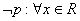 ,均有
,均有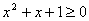
D、若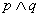 为假命题,则
为假命题,则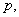
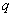 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
下面几种推理过程是演绎推理的是( )
A.某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推各班人数都超过50人
B.由三角形的性质,推测空间四面体的性质
C.平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D.在数列{an}中,a1=1,an=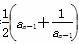 ,由此归纳出{an}的通项公式
,由此归纳出{an}的通项公式
查看答案和解析>>
科目:高中数学 来源: 题型:
考察下列一组不等式:
23+53>22×5+2×52,
34+64>3×63+33×6,
55+95>52×93+53×92,
6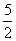 +7
+7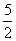 >62×7
>62×7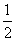 +6
+6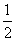 ×72,
×72,
…
将上述不等式在左、右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出平面区域G,如图所示,其中A(5,3),B(2,1),C(1,5).若使目标函数P=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
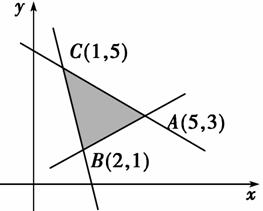
A.4 B.2 C.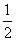 D.
D.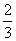
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线的方程是16x2-9y2=144.
(1)求双曲线的焦点坐标、离心率和渐近线方程;
(2)设F1和F2是双曲线的左、右焦点,点P在双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com