
分析 判断f(x)的单调性,求出f(x)的极值,根据零点个数及零点的范围和单调性得出f(-2)>0,从而得出m的范围.
解答 解:解:∵f(x)=x•ex-m,
∴f′(x)=ex+xex=ex(x+1),
∴当x∈(-∞,-1)时,f′(x)<0;
当x∈(-1,+∞)时,f′(x)>0;
∴f(x)在(-∞,-1)上是减函数,在(-1,+∞)上是增函数,
∴当x=-1时,f(x)取得最小值f(-1)=-$\frac{1}{e}$-m,
且当x→-∞时,f(x)→-m,x→+∞时,f(x)→+∞,
∵f(x)有两个零点,∴f(x)在(-∞,-1)和(-1,+∞)上各有1个零点.
∴$\left\{\begin{array}{l}{-m>0}\\{-\frac{1}{e}-m<0}\end{array}\right.$,解得-$\frac{1}{e}$<m<0,
∵f(x)的零点都大于-2,
∴f(-2)>0,即$\frac{-2}{{e}^{2}}$-m>0,解得m<-$\frac{2}{{e}^{2}}$.
故答案为(-$\frac{1}{e}$,-$\frac{2}{{e}^{2}}$).
点评 本题考查了函数单调性、极值与函数零点的关系,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
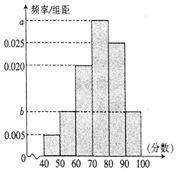 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y-3)2=5 | B. | x2+(y+3)2=5 | C. | (x-3)2+y2=5 | D. | (x+3)2+y2=5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com