
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 (1)不正确,例如$\frac{7π}{3}$是第一象限角但是不是锐角;
(2)角α终边经过点(a,a)(a≠0)时,sinα+cosα=±$\sqrt{2}$,即可判断出正误;
(3)由y=$\frac{1}{2}$sin(ωx)的最小正周期为4π,则ω=±$\frac{1}{2}$,即可判断出正误;
(4)若cos(α+β)=-1,则α+β=2kπ+π(k∈Z),α=2kπ+π-β,代入计算即可得出.
解答 解:(1)第一象限角是锐角,不正确,例如$\frac{7π}{3}$是第一象限角但是不是锐角,因此不正确;
(2)角α终边经过点(a,a)(a≠0)时,sinα+cosα=±$\sqrt{2}$,因此不正确;
(3)若y=$\frac{1}{2}$sin(ωx)的最小正周期为4π,则ω=±$\frac{1}{2}$,因此不正确;
(4)若cos(α+β)=-1,则α+β=2kπ+π(k∈Z),∴α=2kπ+π-β,∴sin(2α+β)+sinβ=sin(4kπ+2π-2β+β)+sinβ=-sinβ+sinβ=0,正确.
故选:B.
点评 本题考查了简易逻辑的判定方法、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
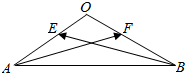 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [0,1] | C. | [0,3] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{8}$) | B. | ($\frac{1}{4}$,0) | C. | (1,0) | D. | (0,$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | -3 | C. | 6 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com