
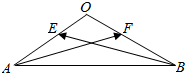
 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10. 分析 根据向量的加减的几何意义和向量的数量积即可求出答案.
解答 解:∵等腰△OAB中,∠A=∠B=30°,|$\overrightarrow{OA}$|=2,
∴|$\overrightarrow{OB}$|=2,∠AOB=120°,
∴$\overrightarrow{AF}$•$\overrightarrow{AB}$=($\overrightarrow{OF}$-$\overrightarrow{OA}$)($\overrightarrow{OB}$-$\overrightarrow{OA}$)=(μ$\overrightarrow{OB}$-$\overrightarrow{OA}$)($\overrightarrow{OB}$-$\overrightarrow{OA}$)=μ($\overrightarrow{OB}$)2-(μ+1)$\overrightarrow{OA}$•$\overrightarrow{OB}$+($\overrightarrow{OA}$)2=4μ-(μ+1)×2×2×(-$\frac{1}{2}$)+4=6μ+6=9,
∴μ=$\frac{1}{2}$;
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=($\overrightarrow{OF}$-$\overrightarrow{OA}$)($\overrightarrow{OE}$-$\overrightarrow{OB}$)(μ$\overrightarrow{OB}$-$\overrightarrow{OA}$)(λ$\overrightarrow{OA}$-$\overrightarrow{OB}$)=(λμ+1)$\overrightarrow{OA}$•$\overrightarrow{OB}$-λ($\overrightarrow{OA}$)2-μ($\overrightarrow{OB}$)2=-2(λμ+1)-4λ-4μ,
∵λ+2μ=2,
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=λ2-4λ-6=(λ-2)2-10,
当λ=2时,有最小值为-10,
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10,
故答案为:$\frac{1}{2}$,-10.
点评 本题考查了向量的加减的几何意义和向量的数量积,以及函数的性质,培养了学生的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
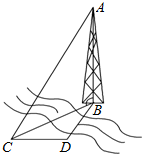 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com