
分析 先求导数$y′=\frac{-a}{2(a-1)\sqrt{3-ax}}$,根据题意便可得到$\frac{-a}{a-1}<0$,从而解出a<0,或a>1①,还需满足3-ax≥0在x∈(0,1]上恒成立,这样便得到$a≤\frac{3}{x}$在x∈(0,1]上恒成立,从而得出a≤3②,这样由①②便可得出a的取值范围.
解答 解:$y′=\frac{-a}{2(a-1)\sqrt{3-ax}}$;
原函数在(0,1]上是减函数;
∴y′<0;
∴$\frac{-a}{a-1}<0$;
解得a<0,或a>1;
且3-ax≥0在x∈(0,1]上恒成立;
即$a≤\frac{3}{x}$在x∈(0,1]上恒成立;
$y=\frac{3}{x}$在(0,1]上的最小值为3;
∴a≤3,又a<0,或a>1;
∴a<0,或1<a≤3;
∴a的取值范围为(-∞,0)∪(1,3].
故答案为:(-∞,0)∪(1,3].
点评 考查函数单调性和函数导数符号的关系,分式不等式的解法,以及反比例函数的单调性,根据函数单调性求最值.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
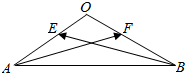 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10) | B. | (-10,-1) | C. | $(0,\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}})$ | D. | $(-10,\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [0,1] | C. | [0,3] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com