
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 设D是BC的中点,A A’与面PBC交于O,推导出A’A=A’B=CA=CB=1,从而得到AB⊥平面A′CE,由此能求出A’C与AB所成角.
解答 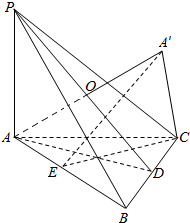 解:设D是BC的中点,A A’与面PBC交于O,
解:设D是BC的中点,A A’与面PBC交于O,
∵△ABC是边长为1的正三角形,PA⊥平面ABC,且PA=$\frac{\sqrt{6}}{2}$,点A关于平面PBC的对称点为A′,
∴O必在PD上,AA′⊥平面PBC,
∴∠AOD=∠PAD=90°,∠ODA=∠PDA,
∴△ADO∽△PDA,∴$\frac{AO}{AD}=\frac{PA}{PD}$,
∵AD=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,PA=$\frac{\sqrt{6}}{4}$,
∴PD=$\sqrt{\frac{3}{4}+\frac{3}{8}}$=$\frac{3\sqrt{2}}{4}$,AO=$\frac{\frac{\sqrt{6}}{4}×\frac{\sqrt{3}}{2}}{\frac{3\sqrt{2}}{4}}$=$\frac{1}{2}$,AA′=1,
∵又A与A’关于平面PBC对称,
∴A′B=AB=1,
∵A’A=A’B=CA=CB=1,
取AB中点E,连结A′E,CE,
则A′E⊥AB,CE⊥AE,又A′E∩CE=E,
∴AB⊥平面A′CE,∴A’C⊥AB,
∴A’C与AB所成角为$\frac{π}{2}$.
故选:D.
点评 本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
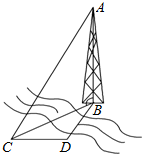 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
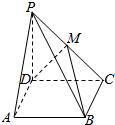 已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.
已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com