
分析 (Ⅰ)通过q是否为1,利用错位相减法求解数列{an}的前n项和Sn公式;
(Ⅱ)设q≠1,求出数列$\left\{{\frac{S_n}{n}}\right\}$的钱3项,利用等比中项,推出矛盾,说明不是等比数列.
解答 解:设{an}的前n项和为Sn,
当q=1时,${S_n}={a_1}+{a_1}q+…+{a_1}{q^{n-1}}=n{a_1}$;--------------------(1分)
当q≠1时,${S_n}={a_1}+{a_1}q+…+{a_1}{q^{n-1}}$. ①
$q{S_n}={a_1}q+…+{a_1}{q^{n-1}}+{a_1}{q^n}$,②----------------(3分)
①-②得$({1-q}){S_n}={a_1}({1-{q^n}})$,所以 ${S_n}=\frac{{{a_1}({1-{q^n}})}}{1-q}$.----------(5分)
所以 ${S_n}=\left\{\begin{array}{l}n{a_1},q=1\\ \frac{{{a_1}({1-{q^n}})}}{1-q},q≠1.\end{array}\right.$----------------------------(7分)
(Ⅱ)证:由{an}是公比为q的等比数列有a1≠0,若对任意的n∈N+,数列$\left\{{\frac{S_n}{n}}\right\}$是等比数列,则考虑数列$\left\{{\frac{S_n}{n}}\right\}$的前三项,有${[{\frac{{{a_1}({1-{q^2}})}}{1-q}}]^2}=\frac{a_1}{1}•\frac{{{a_1}({1-{q^3}})}}{1-q}$,--------------------(9分)
化简得 q2-2q+1=0,即(q-1)2=0,----------------(10分)
但q≠1时,(q-1)2>0,
这一矛盾说明数列$\left\{{\frac{S_n}{n}}\right\}$不是等比数列.---------------------(12分)
点评 本题考查数列求和等比数列的判断与证明,考查逻辑推理能力以及计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相交 | C. | 内切 | D. | 外切 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
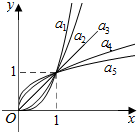 如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质:
如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com