
分析 (1)通过a3=log2$\frac{{b}_{3}}{{b}_{2}}$=log264=6及a1=2可得d=2,进而可得an=2n,利用a1+a2+a3+…+an=log2bn可得bn=2n(n+1);
(2)通过(I)及cn=(an+n+1)•2an-2可得Tn、4Tn的表达式,利用错位相减法计算即得结论.
解答 解:(1)由已知可得:a1+a2+a3=log2b3,a1+a2=log2b2,
两式相减可得:a3=log2$\frac{{b}_{3}}{{b}_{2}}$=log264=6,
∵a1=2,∴d=$\frac{{a}_{3}-{a}_{1}}{3-1}$=2,∴an=2n;
∵a1+a2+a3+…+an=2•$\frac{n(n+1)}{2}$=n(n+1)=log2bn,
∴bn=2n(n+1);
(2)由题意cn=(an+n+1)•2an-2=(3n+1)4n-1,
∴Tn=4+7•4+10•42+…+(3n+1)•4n-1,
4Tn=4•4+7•42+10•43+…+(3n+1)•4n,
两式相减得:-3Tn=4+3•4+3•42+…+3•4n-1-(3n+1)•4n
=4+3(4+42+…+4n-1)-(3n+1)•4n
=4+3•$\frac{4(1-{4}^{n-1})}{1-4}$-(3n+1)•4n,
整理得:Tn=n•4n(n∈N*).
点评 本题考查求数列的通项及前n项和公式,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
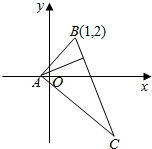 如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:
如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α=0,则sinα≥cosα | B. | 若sinα<cosα,则α≠0 | ||
| C. | 若α≠0,则sinα≥cosα | D. | 若sinα≥cosα,则α≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
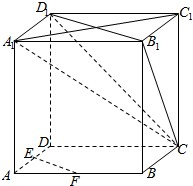 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com