练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．下列计算正确的是（　　）
    A．$\sqrt{{{（{m-n}）}^2}}=m-n$B．log23×log25=log215
    C．210-29=29D．${（{-\frac{125}{27}}）^{\frac{2}{3}}}=-\frac{25}{9}$

    分析 利用指数幂与对数的运算性质即可判断出正误．

    解答 解：A．m＜n时不成立，不正确；
    B．log23×log25=$\frac{lg3}{lg2}•\frac{lg5}{lg2}$≠log215，不正确．
    C.210-29=2•29-29=29
    D.$（-\frac{125}{27}）^{\frac{2}{3}}$=$（\frac{5}{3}）^{3×\frac{2}{3}}$=$\frac{25}{9}$，因此不正确．
    故选：C．

    点评 本题考查了指数幂与对数的运算性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．关于x的方程x2+x+q=0（q∈[0，1]）有实根的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{1}{4}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知数列{an}与{bn}满足：a1+a2+a3+…+an=log2bn（n∈N*），且数列{an}为等比数列，a1=2，b3=64b2．
    （1）求an和bn；
    （2）设cn=（an+n+1）•2an-2，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．圆心为C的圆经过点A（0，2）和点B（2，0），且圆心C在直线l1：2x-y-4=0上．
    （Ⅰ） 求圆C的方程；
    （Ⅱ） 求直线l2：3x+4y-8=0被圆C截得的弦的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

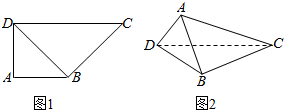    15．如图，在直角梯形ABCD中，AB⊥AD，AB=AD=2，CD=4，将三角形ABD沿BD翻折，使面ABD⊥面BCD．
    （Ⅰ） 求线段AC的长度；
    （Ⅱ） 求证：AD⊥平面ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

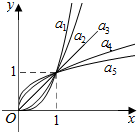    5．如图是幂函数$y={x^{α_i}}$（αi＞0，i=1，2，3，4，5）在第一象限内的图象，其中α1=3，α2=2，α3=1，${α_4}=\frac{1}{2}$，${α_5}=\frac{1}{3}$，已知它们具有性质：
    ①都经过点（0，0）和（1，1）；   ②在第一象限都是增函数．
    请你根据图象写出它们在（1，+∞）上的另外一个共同性质：α越大函数增长越快．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设Sn为等比数列{an}的前n项和，且8a3+a6=0，则$\frac{S_4}{S_2}$=（　　）
    A．-11B．-8C．5D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知对数函数f（x）图象经过点（8，3）
    （I）求函数f（x）的解析式；
    （II）若f（x）＞1，求x的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=x3-bx2-4，x∈R，则下列命题正确的是（　　）
    A．当b＞0时，?x0＜0，使得f（x0）=0
    B．当b＜0时，?x＜0，都有f（x）＜0
    C．f（x）有三个零点的充要条件是b＜-3
    D．f（x）在区间（0．+∞）上有最小值的充要条件是b＜0

    查看答案和解析>>

    同步练习册答案