
分析 (Ⅰ) 根据圆的性质或者利用待定系数法即可求圆C的方程;
(Ⅱ)根据直线和圆相交的弦长公式进行求解即可.
解答 解:(Ⅰ) 解法1:AB的中点为(1,1),斜率为-1,则AB的垂直平分线为y=x.…(2分)
联立$\left\{\begin{array}{l}y=x\\ 2x-y-4=0\end{array}\right.$,解得圆心C的坐标为(4,4).…(5分)
半径$r=\sqrt{{{({4-0})}^2}+{{({4-2})}^2}}=2\sqrt{5}$,所以圆C的方程为(x-4)2+(y-4)2=20.…(7分)
解法2:设圆C的方程为x2+y2+Dx+Ey+F=0.…(1分)
由$\left\{\begin{array}{l}4+2E+F=0\\ 4+2D+F=0\\ 2({-\frac{D}{2}})-({-\frac{E}{2}})-4=0\end{array}\right.$,解得$\left\{\begin{array}{l}D=-8\\ E=-8\\ F=12\end{array}\right.$,故所求圆C的方程为x2+y2-8x-8y+12=0.…(7分)
(Ⅱ)圆心到l2的距离为$d=\frac{{|{3×4+4×4-8}|}}{{\sqrt{{3^2}+{4^2}}}}=4$.…(9分)
所以弦长的一半为$\sqrt{{r^2}-{d^2}}=\sqrt{20-16}=2$,于是直线l2被圆C截得的弦的长度为4.…(12分)
点评 本题主要考查圆的方程的求解,以及直线和圆相交时弦长公式的计算,考查学生的运算能力.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
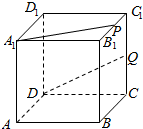 如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)
如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
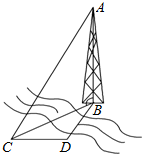 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com