
分析 (1)通过讨论a的范围,得到不等式组,解出即可;(2)分别求出p,q真时的a的范围,再根据p真q假或p假q真得到a的范围.
解答 解:(1)由题意ax2-x+$\frac{1}{16}$a>0对任意x∈R恒成立,
当a=0时,不符题意,舍去;
当a≠0时,则$\left\{\begin{array}{l}{a>0}\\{△=1-4a•\frac{1}{16}a<0}\end{array}\right.$
解得:a>2.
∴实数a的取值范围是a>2;
(2)由双曲线:$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{a}$=1的离心率e∈(1,2),
∴e2=$\frac{5+a}{5}$.
∵离心率e∈(1,2),
∴1<$\frac{5+a}{5}$<4.
∴0<a<15.
∴a的取值范围为(0,15).
p真q假时,a≥15,p假p真时,则0<a≤2,
综上,0<a≤2或a≥15.
点评 本题考查了复合命题的判断,考查对数函数、双曲线的性质,是一道基础题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
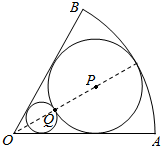 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com