分析:(1)假设直线AB1与BC1不是异面直线,它们都在平面α上,推出平面ABB1A1和平面BCC1B1重合,这是矛盾,
(2)求出平面的一个法向量,直线和平面所成的角的余弦值等于直线与平面的法向量夹角的正弦值.
解答: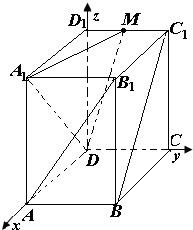
证明:(1)(反证法)假设直线AB
1与BC
1不是异面直线.(1分)
设直线AB
1与BC
1都在平面α上,则A、B、B
1、C
1∈α.(3分)
因此,平面ABB
1A
1、平面BCC
1B
1都与平面α有不共线的三个公共点,
即平面ABB
1A
1和平面BCC
1B
1重合(都与平面α重合).又长方体的相邻两个面不重合,这是矛盾,
于是,假设不成立.(6分)
所以直线AB
1与BC
1是异面直线.(7分)
解:(2)按如图所示建立空间直角坐标系,
可得有关点的坐标为D(0,0,0)、
A(4,0,0)、B(4,2,0),C(0,2,0),A
1(4,0,4),B
1(4,2,4),C
1(0,2,4),D
1(0,0,4).于是,M(0,1,4),
=(0,1,4),=(4,0,4),=(0,2,4).(9分)
设平面DA
1M的法向量为
=(x,y,z),则
,即
.
取z=-1,得x=1,y=4.(11分)
所以平面DA
1M的一个法向量为
=(1,4,-1).
记直线AB
1与平面DA
1M所成角为θ,于是,
sinθ=||=,
θ=arcsin.(13分)
所以,直线AB
1与平面DA
1M所成角为θ=
arcsin.(14分)
点评:本题考查用反证法证明2条直线是异面直线、及用向量法求直线和平面的夹角.

 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点. 证明:(1)(反证法)假设直线AB1与BC1不是异面直线.(1分)
证明:(1)(反证法)假设直线AB1与BC1不是异面直线.(1分)

 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=
已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC= 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.