
【题目】已知函数![]() 有两个零点
有两个零点![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)证明:![]() .
.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,离心率为
,离心率为![]() .已知
.已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 到抛物线的准线
到抛物线的准线![]() 的距离为
的距离为![]() .
.
(I)求椭圆的方程和抛物线的方程;
(II)设![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.沿
的中点.沿![]() 将矩形
将矩形![]() 折起,使
折起,使![]() ,如图所示.设P、Q分别为线段
,如图所示.设P、Q分别为线段![]() ,
,![]() 的中点,连接
的中点,连接![]() .
.
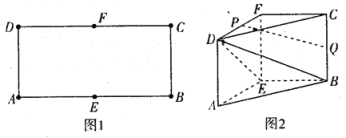
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为![]() 米,高为
米,高为![]() 米,体积为
米,体积为![]() 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为![]() 元(
元(![]() 为圆周率).该蓄水池的体积最大时
为圆周率).该蓄水池的体积最大时![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,E,F分别为
中,E,F分别为![]() 的三等分点,
的三等分点,![]() ,
,![]() ,
,![]() ,
,![]() ,若沿着
,若沿着![]() ,
,![]() 折叠使得点A和点B重合,如图2所示,连结
折叠使得点A和点B重合,如图2所示,连结![]() ,
,![]() .
.
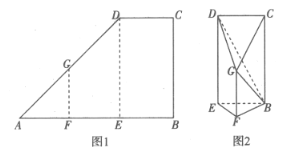
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,湖中有一个半径为![]() 千米的圆形小岛,岸边点
千米的圆形小岛,岸边点![]() 与小岛圆心
与小岛圆心![]() 相距
相距![]() 千米,为方便游人到小岛观光,从点
千米,为方便游人到小岛观光,从点![]() 向小岛建三段栈道
向小岛建三段栈道![]() ,
,![]() ,
,![]() ,湖面上的点
,湖面上的点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 均与圆
均与圆![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中栈道
,其中栈道![]() ,
,![]() ,
,![]() 和小岛在同一个平面上.沿圆
和小岛在同一个平面上.沿圆![]() 的优弧(圆
的优弧(圆![]() 上实线部分)上再修建栈道
上实线部分)上再修建栈道![]() .记
.记![]() 为
为![]() .
.
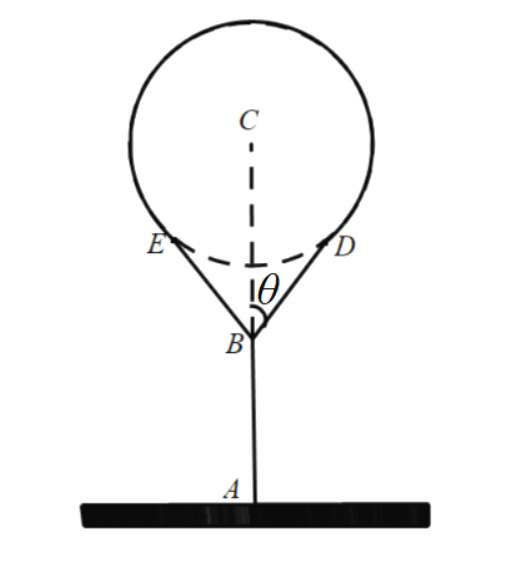
![]() 用
用![]() 表示栈道的总长度
表示栈道的总长度![]() ,并确定
,并确定![]() 的取值范围;
的取值范围;
![]() 求当
求当![]() 为何值时,栈道总长度最短.
为何值时,栈道总长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,E,F分别为AB的三等分点,
中,E,F分别为AB的三等分点,![]() ,
,![]() ,
,![]() ,
,![]() 若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
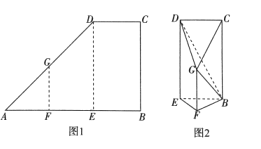
(1)求证:平面![]() 平面BCDE;
平面BCDE;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com