练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知向量$\overrightarrow{OM}=（3，-2），\overrightarrow{ON}=（-5，-1），则\overrightarrow{MN}等于$（　　）
    A．（8，-1）B．（-8，1）C．（-2，-3）D．（-15，2）

    分析 根据题意，由向量的三角形法则可得$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$，将向$\overrightarrow{OM}$、$\overrightarrow{ON}$的坐标代入，计算可得答案．

    解答 解：根据题意，$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$，
    又由向量$\overrightarrow{OM}$=（3，-2），$\overrightarrow{ON}$=（-5，-1）；
    则$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=（-8，1）；
    故选：B．

    点评 本题考查向量的坐标运算，要掌握向量的三角形法则．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知双曲线x2-y2=1，点F1，F2为其两个焦点，点P为双曲线上一点，若|PF1|=1，则|PF2|=（　　）
    A．3B．$2\sqrt{2}$C．4D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

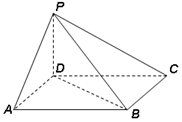    5．如图四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2PD=2，PD⊥面ABCD．
    （I）证明：PA⊥BD；
    （II）若PD=AD，求二面角A-PB-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．毕业临近，5位同学按顺序站成一排合影留念，其中2位女同学，3位男同学，则女生甲不站两端，3位男同学有且只有2位相邻的排法总数有（　　）种．
    A．24B．36C．48D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．运行如图所示的程序框图，则输出的结果S=（　　）
    A．1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$B．$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$C．1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$D．$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数$f（x）=cos（2x-\frac{π}{3}）+2{sin^2}x$．
    （Ⅰ）求函数f（x）的周期、单调递增区间；
    （Ⅱ）当x∈$[0，\frac{π}{2}]$时，求函数f（x）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若圆x2+（y-1）2=3截直线y=kx-1所得的弦长为2，则斜率k的值是（　　）
    A．$±\sqrt{2}$B．$±\sqrt{3}$C．±1D．±2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

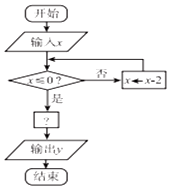    3．如图是一个算法的程序框图，当输入的x的值为7时，输出的 y值恰好是-1，则“？”处应填的关系式可能是（　　）
    A．y=2x+1B．y=3-xC．y=|x|D．y=log${\;}_{\frac{1}{3}}$x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=（t+1）lnx+tx2+3t，t∈R．
    （1）若t=0，求证：当x≥0时，f（x+1）≥x-$\frac{1}{2}$x2；
    （2）若f（x）≥4x对任意x∈[1，+∞）恒成立，求t的取值范围．

    查看答案和解析>>

    同步练习册答案