
分析 (1)由数列{an}满足a1=2,$\frac{{a}_{n+1}}{2}$=$\frac{{a}_{n}}{{a}_{n}+2}$,两边取倒数,再利用等差数列的通项公式即可得出;
(2)利用等比数列的通项公式可得bn,再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵数列{an}满足a1=2,$\frac{{a}_{n+1}}{2}$=$\frac{{a}_{n}}{{a}_{n}+2}$,
∴$\frac{2}{{a}_{n+1}}=1+\frac{2}{{a}_{n}}$,
化为$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{2}$,
∴数列$\{\frac{1}{{a}_{n}}\}$是等差数列,首项与公差都为$\frac{1}{2}$,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{2}+(n-1)×\frac{1}{2}$=$\frac{n}{2}$.
∴an=$\frac{2}{n}$.
(2)∵等比数列{bn}的公比为3,且b1+b3=10.
∴${b}_{1}(1+{3}^{2})$=10,
解得b1=1.
∴bn=3n-1.
cn=$\frac{3{b}_{n}}{{a}_{n}}$=$\frac{{n•3}^{n}}{2}$,
∴数列{cn}的前n项和Tn=$\frac{1}{2}(3+2×{3}^{2}+…+n•{3}^{n})$,
3Tn=$\frac{1}{2}({3}^{2}+2×{3}^{3}+…+n•{3}^{n+1})$,
∴-2Tn=$\frac{1}{2}(3+{3}^{2}+…+{3}^{n}-n•{3}^{n+1})$=$\frac{1}{2}(\frac{3({3}^{n}-1)}{3-1}-n•{3}^{n+1})$,
化为Tn=$\frac{2n-1}{8}•{3}^{n+1}$+$\frac{3}{8}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
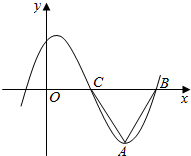 已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.
已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
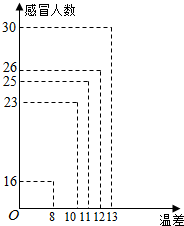 近五天某市气温变化异常,昼夜温差越来越大,感冒的学生较多,该市某校教学兴趣小组从气象站与校医室分别收集了近五天的昼夜温差大小与患感冒人数的数据,得到了如下的散点图:该兴趣小组确定的研究方案是:先从这五组数据中选取两组,用剩下的三组数据求线性回归方程,再对被选取的两组数据进行险验.
近五天某市气温变化异常,昼夜温差越来越大,感冒的学生较多,该市某校教学兴趣小组从气象站与校医室分别收集了近五天的昼夜温差大小与患感冒人数的数据,得到了如下的散点图:该兴趣小组确定的研究方案是:先从这五组数据中选取两组,用剩下的三组数据求线性回归方程,再对被选取的两组数据进行险验.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com