
【题目】已知函数![]()
(1)证明:当![]() 时,
时, ![]() ;
;
(2)若当![]() 时,
时, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析函数单调性变化规律,确定函数最小值为![]() ,即证得结论(2)先讨论分母正负,化分式为整式,再求
,即证得结论(2)先讨论分母正负,化分式为整式,再求![]() 导数,由于
导数,由于![]() ,所以
,所以![]() 必须为增函数,根据单调性讨论可得实数
必须为增函数,根据单调性讨论可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时, ![]() ,
,
则![]() ,令
,令![]() ,解得
,解得![]()
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上是增函数;
上是增函数;
故![]() 在
在![]() 处取得最小值
处取得最小值![]() ,即
,即![]() .
.
(2)由已知![]() ,∴
,∴![]() .
.
(i)当![]() 时,若
时,若![]() ,则
,则![]() ,此时
,此时![]() ,不符合题设条件;
,不符合题设条件;
(ii)当![]() 时,若
时,若![]() ,
, ![]()
令![]() ,则
,则![]()
而![]() .
.
①当![]() 时,由(1)知,
时,由(1)知, ![]() ,即
,即![]() ,
,
它等价于![]() ,
, ![]()
∴![]()
![]()
此时![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() ,即
,即![]() .
.
②当![]() 时,由(1)知,
时,由(1)知, ![]() ,∴
,∴ ![]()
∴![]()
![]()
![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,即
,即![]() ,不符合题设条件.
,不符合题设条件.
综上: ![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+2|+|x-2|,x∈R,不等式f(x)≤6的解集为M.
(1)求M;
(2)当a2,b2∈M时,证明: ![]() |a+b|≤|ab+3|.
|a+b|≤|ab+3|.
查看答案和解析>>
科目:高中数学 来源: 题型:
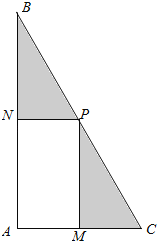
【题目】某学校为进行“阳光运动一小时”活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的矩形
(平方米)的矩形![]() 健身场地。如图,点
健身场地。如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() 米,
米,![]() 米,
米,![]() ,设矩形
,设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正的常数).
为正的常数).
(1)试用![]() 表示
表示![]() ,并指出如何设计矩形的长和宽,才能使得矩形的面积最大,且求出
,并指出如何设计矩形的长和宽,才能使得矩形的面积最大,且求出![]() 的最大值;
的最大值;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ,说明如何选取
,说明如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价).
最低(不要求求出最低造价).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
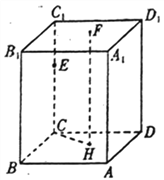
【题目】如图所示,直平行六面体![]() 中,
中,![]() 为棱
为棱![]() 上任意一点,
上任意一点,![]() 为底面
为底面![]() (除
(除![]() 外)上一点,已知
外)上一点,已知![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,若再增加一个条件,就能得到
,若再增加一个条件,就能得到![]() ,现给出以下条件:
,现给出以下条件:
①![]() ;②
;②![]() 在
在![]() 上;③
上;③![]() 平面
平面![]() ;④直线
;④直线![]() 和
和![]() 在平面
在平面![]() 的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(Ⅰ)求所取3张卡片上的数字完全相同的概率;
(Ⅱ)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共14分)如图,在三棱锥![]() 中,
中, ![]() 底面
底面
![]() ,点
,点![]() ,
, ![]() 分别在棱
分别在棱![]() 上,且
上,且![]() (Ⅰ)求证:
(Ⅰ)求证: ![]() 平面
平面![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;(Ⅲ)是否存在点
所成的角的大小;(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com