
【题目】(1)直线![]() 在矩阵
在矩阵![]() 所对应的变换
所对应的变换![]() 下得到直线
下得到直线![]() ,求
,求![]() 的方程.
的方程.
(2)已知点![]() 是曲线
是曲线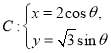 (
(![]() 为参数,
为参数,![]() )上一点,
)上一点,![]() 为坐标原点直线
为坐标原点直线![]() 的倾斜角为
的倾斜角为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)求不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)
;(2)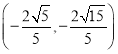 ;(3)
;(3)![]()
【解析】
(1)先在直线![]() 上取点
上取点![]() ,
,![]() 在矩阵
在矩阵![]() 的变换下得到
的变换下得到![]() ,再在直线
,再在直线![]() 上取点
上取点![]() ,在矩阵
,在矩阵![]() 的变换下得到
的变换下得到![]() ,进而可求出
,进而可求出![]() 的方程;
的方程;
(2)根据曲线的参数方程,得到普通方程,根据题意得到直线的直角坐标方程,两式联立,即可求出结果;
(3)分![]() ,
,![]() ,
,![]() 三种情况讨论,分别求解,即可求出结果.
三种情况讨论,分别求解,即可求出结果.
(1)解:在直线![]() 上取点
上取点![]() ,
,
![]() ,故
,故![]() 在矩阵
在矩阵![]() 的变换下得到
的变换下得到![]() ,
,
再在直线![]() 上取点
上取点![]() ,
,
![]() ,在矩阵
,在矩阵![]() 的变换下得到
的变换下得到![]() ,
,
连接![]() ,可得直线
,可得直线![]() .
.
(2)解:由题意得,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立方程组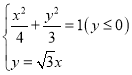 ,解得
,解得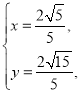 (舍去),或
(舍去),或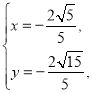
故点![]() 的直角坐标为
的直角坐标为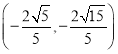 .
.
(3)解:①当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
②当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
③当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上,原不等式的解集为![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)若数列![]() 的首项为
的首项为![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,
,![]() 构成公比小于0的等比数列,求
构成公比小于0的等比数列,求![]() 的值;
的值;
(2)若![]() 是公差为d(d>0)的等差数列
是公差为d(d>0)的等差数列![]() 的前n项和,求
的前n项和,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,且数列
,且数列![]() 单调递增,数列
单调递增,数列![]() 单调递减,求数列
单调递减,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点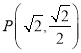 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .
.
(i)证明:直线![]() 与坐标轴平行;
与坐标轴平行;
(ii)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人承包了一块矩形土地![]() 用来种植草莓,其中
用来种植草莓,其中![]() m,
m,![]() m.现规划建造如图所示的半圆柱型塑料薄膜大棚
m.现规划建造如图所示的半圆柱型塑料薄膜大棚![]() 个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米
个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米![]() 元;另外,还需在每个大棚之间留下
元;另外,还需在每个大棚之间留下![]() m宽的空地用于建造排水沟与行走小路(如图中
m宽的空地用于建造排水沟与行走小路(如图中![]() m),这部分建设造价为每平方米
m),这部分建设造价为每平方米![]() 元.
元.
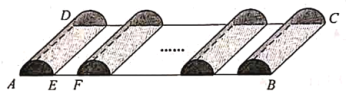
(1)当![]() 时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留
时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留![]() )
)
(2)试确定大棚的个数,使得上述两项费用的和最低?(本小题计算中![]() 取
取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过焦点
过焦点![]() 且与抛物线交于
且与抛物线交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 的倾斜角为30°时,
的倾斜角为30°时,![]() .
.
(1)求抛物线方程.
(2)在平面直角坐标系![]() 中,是否存在定点
中,是否存在定点![]() ,当直线
,当直线![]() 绕
绕![]() 旋转时始终都满足
旋转时始终都满足![]() 平分
平分![]() .若存在,求出
.若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
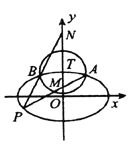
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个不同平面![]() 、
、![]() 、
、![]() 和直线
和直线![]() ,下面有四个命题:
,下面有四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②直线![]() 上有两点到平面
上有两点到平面![]() 的距离相等,则
的距离相等,则![]() ;
;
③![]() ,
,![]() ,则
,则![]() ;
;
④若直线![]() 不在平面
不在平面![]() 内,
内,![]() ,
,![]() ,则
,则![]() .
.
则正确命题的序号为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com