
求值
(1)已知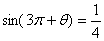 ,
,
求 的值;
的值;
(2)已知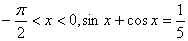 ,求
,求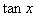 的值。
的值。
科目:高中数学 来源: 题型:解答题
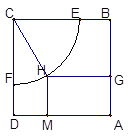
在申办国家级示范性高中期间,某校拟用运动场的边角地建一个矩形的健身室. 如图所示,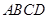 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形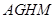 就是拟建的健身室,其中
就是拟建的健身室,其中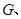
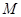 分别在
分别在 和
和 上,
上,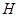 在弧
在弧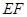 上,设矩形
上,设矩形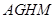 的面积为
的面积为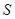 ,∠
,∠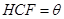 .
.
(1) 试将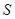 表示为
表示为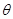 的函数;
的函数;
(2) 当点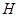 在弧
在弧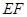 的何处时,该健身室的面积最大?最大面积为多少?
的何处时,该健身室的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=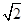 sin
sin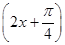 .
.
(1)求它的振幅、周期、初相;
(2)在所给坐标系中用五点法作出它在区间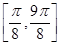 上的图象.
上的图象.
(3)说明y=sin x的图像可由y=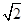 sin
sin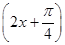 的图像经过怎样的变换而得到.
的图像经过怎样的变换而得到.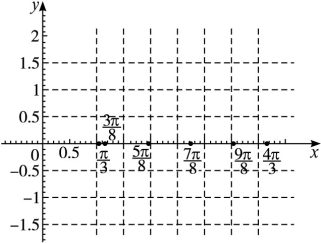
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com