
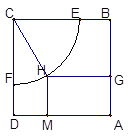
在申办国家级示范性高中期间,某校拟用运动场的边角地建一个矩形的健身室. 如图所示,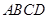 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形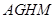 就是拟建的健身室,其中
就是拟建的健身室,其中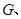
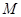 分别在
分别在 和
和 上,
上,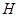 在弧
在弧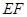 上,设矩形
上,设矩形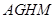 的面积为
的面积为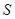 ,∠
,∠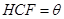 .
.
(1) 试将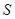 表示为
表示为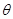 的函数;
的函数;
(2) 当点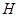 在弧
在弧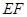 的何处时,该健身室的面积最大?最大面积为多少?
的何处时,该健身室的面积最大?最大面积为多少?
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com