【题目】设
、
是两条不同的直线，
、
是两个不同的平面，则下列四个命题：
①若
，
，则∥②若∥，
，则
③若，，则∥④若，，
，则
其中正确的命题序号是________
字词句段篇系列答案科目：高中数学 来源： 题型：
【题目】某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
（1）分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；
（2）求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精确到0.01）
附：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若实数
满足
，称为函数
的不动点.有下面三个命题：（1）若是二次函数，且没有不动点，则函数
也没有不动点；（2）若是二次函数，则函数可能有
个不动点；（3）若的不动点的个数是
，则的不动点的个数不可能是
；它们中所有真命题的序号是________________________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对定义在
上的函数
和常数
，
，若
恒成立，则称
为函数的一个“凯森数对”.
（1）若
是的一个“凯森数对”，且
，求
；
（2）已知函数
与
的定义域都为，问它们是否存在“凯森数对”？分别给出判断并说明理由；
（3）若
是的一个“凯森数对”，且当
时，
，求在区间
上的不动点个数（函数
的不动点即为方程
的解）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C过点M（0，-2）、N（3，1），且圆心C在直线x+2y+1=0上．
（1）求圆C的方程；
（2）设直线ax-y+1=0与圆C交于A，B两点，是否存在实数a，使得过点P（2，0）的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数
,若存在区间
,使得
,则称函数为“可等域函数”,区间A为函数的一个“可等域区间”.给出下列四个函数:①
;②
;③
;④
.其中存在唯一“可等域区间”的“可等域函数”的个数是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】欧拉公式
（
为虚数单位，
，
为自然底数）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，
表示的复数在复平面中位于（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，已知ABCD为梯形，AB∥CD，CD=2AB，M为线段PC上一点.
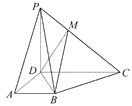
(1)设平面PAB∩平面PDC=l，证明：AB∥l；
(2)在棱PC上是否存在点M，使得PA∥平面MBD，若存在，请确定点M的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四边形
的四个顶点在椭圆
： 
上，对角线
所在直线的斜率为
，且
， 
.
（1）当点
为椭圆
的上顶点时，求
所在直线方程；
（2）求四边形
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
