解:(Ⅰ)
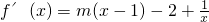
(x>0).
当

时,
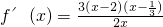
,令f′(x)=0,得x
1=2,x
2=

.
f(x),f′(x)的变化情况如下表:
| x | (0, ) ) |  | ( ,2) ,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以,当x=2时,函数f(x)取到极小值,且极小值为f(2)=ln2-

.(4分)
(Ⅱ)令f′(x)=0,得mx
2-(m+2)x+1=0. (*)
因为△=(m+2)
2-4m=m
2+4>0,所以方程(*)存在两个不等实根,记为a,b(a<b).
因为m≥1,所以

所以a>0,b>0,即方程(*)有两个不等的正根,因此f′(x)<0的解为(a,b).
故函数f(x)存在单调递减区间.(8分)
(Ⅲ)因为f′(1)=-1,所以曲线C:y=f(x)在点P(1,1)处的切线l为y=-x+2.
若切线l与曲线C只有一个公共点,则方程

m(x-1)
2-2x+3+lnx=-x+2有且只有一个实根.
显然x=1是该方程的一个根.
令g(x)=

m(x-1)
2-x+1+lnx,则

.
当m=1时,有g′(x)≥0恒成立,所以g(x)在(0,+∞)上单调递增,所以x=1是方程的唯一解,m=1符合题意.
当m>1时,令g′(x)=0,得x
1=1,x
2=

,则x
2∈(0,1),易得g(x)在x
1处取到极小值,在x
2处取到极大值.
所以g(x
2)>g(x
1)=0,又当x→0时,g(x)→-∞,所以函数g(x)在(0,

)内也有一个解,即当m>1时,不合题意.
综上,存在实数m,当m=1时,曲线C:y=f(x)在点P(1,1)处的切线l与C有且只有一个公共点.(14分)
分析:(I)先求出导函数,然后求出f′(x)=0,通过列表判定函数的单调性,从而确定函数的极小值;
(II)令f′(x)=0,因为△>0,所以方程存在两个不等实根,根据条件进一步可得方程有两个不等的正根,从而得到函数f(x)存在单调递减区间;
(III)先求出函数y=f(x)在点P(1,1)处的切线l的方程,若切线l与曲线C只有一个公共点,则只需方程f(x)=-x+2有且只有一个实根即可.
点评:本题主要考查了利用导数研究函数的极值和单调性,以及导数的几何意义,同时考查了转化的思想,属于中档题.

 m(x-1)2-2x+3+lnx(m≥1).
m(x-1)2-2x+3+lnx(m≥1). 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;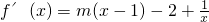 (x>0).
(x>0). 时,
时,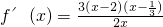 ,令f′(x)=0,得x1=2,x2=
,令f′(x)=0,得x1=2,x2= .
. )
)
 ,2)
,2) .(4分)
.(4分)
 m(x-1)2-2x+3+lnx=-x+2有且只有一个实根.
m(x-1)2-2x+3+lnx=-x+2有且只有一个实根. m(x-1)2-x+1+lnx,则
m(x-1)2-x+1+lnx,则 .
. ,则x2∈(0,1),易得g(x)在x1处取到极小值,在x2处取到极大值.
,则x2∈(0,1),易得g(x)在x1处取到极小值,在x2处取到极大值. )内也有一个解,即当m>1时,不合题意.
)内也有一个解,即当m>1时,不合题意.

 口算能手系列答案
口算能手系列答案