
| A. | e-1 | B. | e+1 | C. | e | D. | $\frac{1}{e}+1$ |
分析 由函数为单调函数可知f(x)-ax为常数,不妨设f(x)=ax+c,于是f(c)=a+1,从而解出c,得出f(x)的解析式,利用定积分可得结论.
解答 解:∵函数f(x)是定义在R上的单调函数,不妨设f(c)=a+1,
∴f(x)-ax=c,即f(x)=ax+c.
∴f(c)=ac+c=a+1.∴c=1.∴f(x)=ax+1.
∴${∫}_{0}^{1}$f(x)dx=${∫}_{0}^{1}$(ax+1)dx=($\frac{{a}^{x}}{lna}$+x)${|}_{0}^{1}$=$\frac{a}{lna}$+1-$\frac{1}{lna}$,
∵a≥e,e自然数对数的底数,
∴${∫}_{0}^{1}$f(x)dx的最小值为e
故选:C.
点评 本题考查了函数的单调性的性质,考查定积分知识的运用,属于中档题,求出f(x)解析式是关键.


科目:高中数学 来源: 题型:解答题
 有300m长的篱笆材料,如果利用已有的一面墙(设长度够用)作为一边,围成一块矩形的菜地,(如图所示)
有300m长的篱笆材料,如果利用已有的一面墙(设长度够用)作为一边,围成一块矩形的菜地,(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
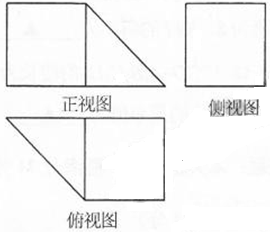 一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )
一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )| A. | $8+8\sqrt{2}\;c{m^2}$ | B. | $12+8\sqrt{2}\;c{m^2}$ | C. | $16+8\sqrt{2}\;c{m^2}$ | D. | $20+8\sqrt{2}\;c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.
如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2{e}^{2}}$,$\frac{1}{e}$) | B. | ($\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | C. | (e,2e) | D. | (e,e3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com