
分析 设该工人在2012年一年里所得奖金为X,则X的可能取值为0,300,750,1260,1800,分别求出相应的概率,由此能求出他在2012年一年里所得奖金的分布列及期望.
解答 解:设该工人在2012年一年里所得奖金为X,
则X是一个离散型随机变量.
由于该工人每季度完成任务与否是等可能的,
所以他每季度完成任务的概率都等于$\frac{1}{2}$,
所以P(X=0)=${C}_{4}^{0}(\frac{1}{2})^{0}(\frac{1}{2})^{4}$=$\frac{1}{16}$,
P(X=300)=${C}_{4}^{1}(\frac{1}{2})(\frac{1}{2})^{3}$=$\frac{1}{4}$,
P(X=750)=${C}_{4}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{2}$=$\frac{3}{8}$,
P(X=1260)=${C}_{4}^{3}(\frac{1}{2})^{3}(\frac{1}{2})$=$\frac{1}{4}$,
P(X=1800)=${C}_{4}^{4}(\frac{1}{2})^{4}(\frac{1}{2})^{0}$=$\frac{1}{16}$.
∴X的分布列为
| X | 0 | 300 | 750 | 1260 | 1800 |
| p | $\frac{1}{16}$ | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{1}{4}$ | $\frac{1}{16}$ |
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 相关系数用来衡量x与y之间的线性相关程度 | |
| B. | |r|≤1,且|r|越接近0,线性相关程度越小 | |
| C. | 若r>0,则x与y是正相关 | |
| D. | |r|≥1,且|r|越接近1,线性相关程度越大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)有唯一的极小值f(2) | B. | f(x)既有极小值f(2)又有极大值f(-1) | ||
| C. | f(x)在(-∞,2)上为增函数 | D. | f(x)在(-∞,-1)∪(-1,2)上为增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
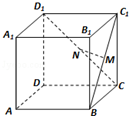 如图,在正方体ABCD-A1B1C1D1中,M、N分别是BC1、CD1的中点,则下列说法错误的是( )
如图,在正方体ABCD-A1B1C1D1中,M、N分别是BC1、CD1的中点,则下列说法错误的是( )| A. | MN∥AB | B. | MN⊥AC | C. | MN⊥CC1 | D. | MN∥平面ABCD |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,0] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com