
���� ��1�����ҽ���F2��c��0����l��y=k��x-c����P��0��-ck�������е����깫ʽ�ɵã�$B��\frac{c}{2}��-\frac{ck}{2}��$������B����Բ�ϣ��ɵ�${k^2}=\frac{{4{b^2}}}{c^2}\frac{{4{a^2}-{c^2}}}{{4{a^2}}}=��\frac{1}{e^2}-1����4-{e^2}��=\frac{4}{e^2}+{e^2}-5$������$|k|��\frac{{2\sqrt{5}}}{5}$��������ɵó���
��2��$k=\frac{{2\sqrt{5}}}{5}$���ɵ�$e=\frac{{2\sqrt{5}}}{5}$����$\frac{c^2}{a^2}=\frac{4}{5}$����Բ����Ϊ${x^2}+5{y^2}=\frac{5}{4}{c^2}$��ֱ��l����Ϊ$y=\frac{{2\sqrt{5}}}{5}��x-c����B��\frac{c}{2}��-\frac{{\sqrt{5}}}{5}c��$������Ϊ$x=\frac{5}{4}c$����A��x0��y0���ɵ�$��\frac{5}{4}c-{x_0}��+��\frac{5}{4}c-\frac{c}{2}��=\frac{9}{5}$�����������Բ�����̼��ɵó���
��� �⣺��1�����ҽ���F2��c��0����l��y=k��x-c����P��0��-ck����
��BΪF2P���е㣬��$B��\frac{c}{2}��-\frac{ck}{2}��$��
��B����Բ�ϣ���$\frac{c^2}{{4{a^2}}}+\frac{{{c^2}{k^2}}}{{4{b^2}}}=1$��
��${k^2}=\frac{{4{b^2}}}{c^2}\frac{{4{a^2}-{c^2}}}{{4{a^2}}}=��\frac{1}{e^2}-1����4-{e^2}��=\frac{4}{e^2}+{e^2}-5$��
��$|k|��\frac{{2\sqrt{5}}}{5}$����$\frac{4}{e^2}+{e^2}-5��\frac{4}{5}$��
�ࣨ5e2-4����e2-5����0����$\frac{4}{5}��{e^2}��1$����$e��[\frac{{2\sqrt{5}}}{5}��1��$��
��2��$k=\frac{{2\sqrt{5}}}{5}$����$e=\frac{{2\sqrt{5}}}{5}$����$\frac{c^2}{a^2}=\frac{4}{5}$����${a^2}=\frac{5}{4}{c^2}��{b^2}=\frac{1}{4}{c^2}$��
��Բ����Ϊ$\frac{x^2}{{\frac{5}{4}{c^2}}}+\frac{y^2}{{\frac{1}{4}{c^2}}}=1$����${x^2}+5{y^2}=\frac{5}{4}{c^2}$��
ֱ��l����Ϊ$y=\frac{{2\sqrt{5}}}{5}��x-c����B��\frac{c}{2}��-\frac{{\sqrt{5}}}{5}c��$������Ϊ$x=\frac{5}{4}c$��
��A��x0��y0����$��\frac{5}{4}c-{x_0}��+��\frac{5}{4}c-\frac{c}{2}��=\frac{9}{5}$��
��${x_0}=2c-\frac{9}{5}��{y_0}=\frac{{2\sqrt{5}}}{5}��c-\frac{9}{5}��$��
�֡�A����Բ�ϣ���${��2c-\frac{9}{5}��^2}+5{[\frac{{2\sqrt{5}}}{5}��c-\frac{9}{5}��]^2}=\frac{5}{4}{c^2}$������c-2����5c-6��=0��
��c=2��$c=\frac{6}{5}$��
������Բ����Ϊ$\frac{x^2}{5}+{y^2}=1$��$\frac{{5{x^2}}}{9}+\frac{25}{9}{y^2}=1$��
���� ���⿼������Բ�Ķ�������̼������ʡ�ֱ������Բ�ཻ���⡢�е����깫ʽ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3 | B�� | ��1 | C�� | ��1���3 | D�� | 1��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-3��x��-1��1��x��2} | B�� | {x|-3��x��-1��1��x��2} | C�� | {x|-3��x��-1��1��x��2} | D�� | {x|-3��x��-1��1��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
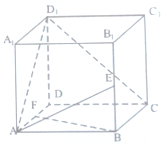 ��ֱ������ABCD-A1B1C1D1�У�AA1=2�������DZ߳�Ϊ1�������壬E��F�ֱ�����B1B��DA���е㣮
��ֱ������ABCD-A1B1C1D1�У�AA1=2�������DZ߳�Ϊ1�������壬E��F�ֱ�����B1B��DA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰?x0��R��ʹ��x02-1��0���ķ��ǡ�?x��R������x2-1��0�� | |
| B�� | ���⡰�����ı���ȵĿռ��ı��β��������Ρ����������Ǽ����� | |
| C�� | ���⡰��x2=y2����x=y������������������� | |
| D�� | ���⡰��x=3����x2-2x-3=0���ķ������ǡ���x��3����x2-2x-3��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ������ | C�� | Բ�� | D�� | Բ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com