
设函数 .
.
(1)当 ,
, 时,求函数
时,求函数 的最大值;
的最大值;
(2)令 ,其图象上存在一点
,其图象上存在一点 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数 的取值范围;
的取值范围;
(3)当 ,
, ,
, 时,方程
时,方程 有唯一实数解,求
有唯一实数解,求 的值.
的值.
(1)函数 的最大值为
的最大值为 ;(2)实数
;(2)实数 的取值范围是
的取值范围是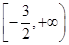 ;(3)
;(3)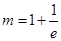 .
.
解析试题分析:(1)将 ,
,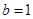 代入函数
代入函数 的解析式,然后利用导数求出函数
的解析式,然后利用导数求出函数 的最大值;(2)先确定函数
的最大值;(2)先确定函数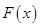 的解析式,并求出函数
的解析式,并求出函数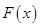 的导数,然后利用导数的几何意义将问题转化为
的导数,然后利用导数的几何意义将问题转化为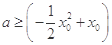 ,利用恒成立的思想进行求解;(3)将
,利用恒成立的思想进行求解;(3)将 ,
, 代入函数
代入函数 的解析式并确定函数
的解析式并确定函数 的解析式,构造新函数
的解析式,构造新函数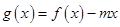 ,利用导数求出函数
,利用导数求出函数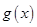 的极值,利用极值为零来求出参数
的极值,利用极值为零来求出参数 的值.
的值.
试题解析:(1)依题意, 的定义域为
的定义域为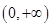 ,
,
当 ,
,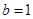 时,
时,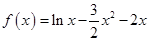 ,
, ,
,
由 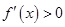 ,得
,得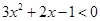 ,解得
,解得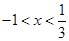 ;
;
由 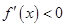 ,得
,得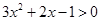 ,解得
,解得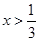 或
或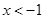 .
.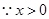 ,
, 在
在 单调递增,在
单调递增,在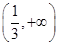 单调递减;
单调递减;
所以 的极大值为
的极大值为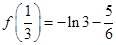 ,此即为最大值;
,此即为最大值;
(2)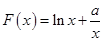 ,
,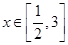 ,则有
,则有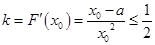 在
在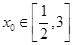 上有解,
上有解,
∴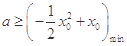 ,
,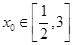
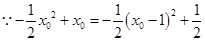 ,
,
所以当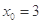 时,
时,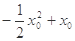 取得最小值
取得最小值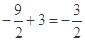 ,
,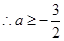 ;
;
(3)因为方程 有唯一实数解,所以
有唯一实数解,所以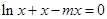 有唯一实数解,
有唯一实数解,
设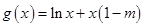 ,则
,则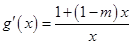 ,
,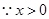 ,
, ,所以由
,所以由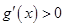 得
得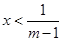 ,
,
由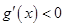 得
得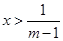 ,所以
,所以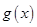 在
在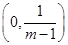 上单调递增,
上单调递增,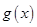 在
在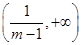 上单调递减,
上单调递减,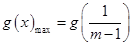 .
.
若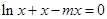 有唯一实数解,则必有
有唯一实数解,则必有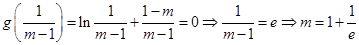 ,
,
所以当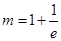 时,方程
时,方程 有唯一实数解.
有唯一实数解.
考点:1.利用导数求函数的最值;2.函数不等式恒成立;3.参数分离法;4.函数的零点


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
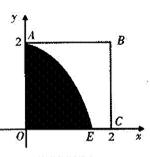
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路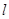 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数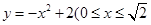 的图象,且点M到边OA距离为
的图象,且点M到边OA距离为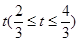 .
.
(1)当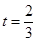 时,求直路
时,求直路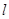 所在的直线方程;
所在的直线方程;
(2)当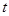 为何值时,地块OABC在直路
为何值时,地块OABC在直路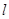 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设a为实数,函数f(x)=ex-2x+2a,x∈R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>ln2-1且x>0时,ex>x2-2ax+1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为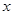 元/本(9≤
元/本(9≤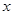 ≤11),预计一年的销售量为
≤11),预计一年的销售量为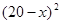 万本.
万本.
(1)求该出版社一年的利润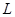 (万元)与每本书的定价
(万元)与每本书的定价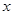 的函数关系式;
的函数关系式;
(2)当每本书的定价为多少元时,该出版社一年的利润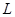 最大,并求出
最大,并求出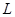 的最大值
的最大值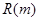 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设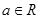 ,函数
,函数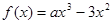 .
.
(1)若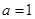 ,求函数
,求函数 的极值与单调区间;
的极值与单调区间;
(2)若函数 的图象在
的图象在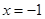 处的切线与直线
处的切线与直线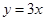 平行,求
平行,求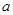 的值;
的值;
(3)若函数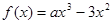 的图象与直线
的图象与直线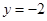 有三个公共点,求
有三个公共点,求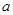 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com