

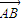 所成比λ的值,求λ值可由已知条件△ADE是△ABC面积一半入手,利用三角形面积比等于三角形相似比的平方关系求得λ,代入定比分点坐标公式,即可求出D点坐标.
所成比λ的值,求λ值可由已知条件△ADE是△ABC面积一半入手,利用三角形面积比等于三角形相似比的平方关系求得λ,代入定比分点坐标公式,即可求出D点坐标. =
= ,
, =
= ,即
,即 =
= .
.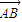 所成的比为λ,利用分点定义,
所成的比为λ,利用分点定义, =
=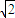 +1.
+1. =2-
=2- ,
, =3-
=3-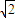 .
. ,3-
,3- ).
). 进行求解.
进行求解. 

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
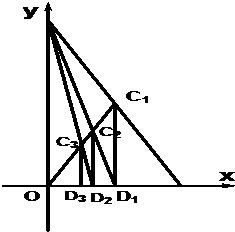 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
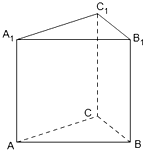 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com