
【题目】已知直角梯形![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角
所成的锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)建立空间直角坐标系,写出相应点的坐标,得到向量![]() ,求出平面平面
,求出平面平面![]() 的法向量,利用向量
的法向量,利用向量![]() 与平面
与平面![]() 垂直,即可证明线面平行;(2)求出平面
垂直,即可证明线面平行;(2)求出平面![]() 与平面
与平面![]() 的法向量,利用法向量所成的角即可求解二面角的余弦值.
的法向量,利用法向量所成的角即可求解二面角的余弦值.
试题解析:(1)设AB=a,取AC的中点O,连接EO,OP.
∵AE=AC,又∠EAC=60°,∴EO⊥AC.
又平面ABC⊥平面ACDE,∴EO⊥平面ABC,∴EO⊥OP,
又OP∥AB,AB⊥AC,所以OP⊥AC.
以射线OP,OC,OE分别为x轴、y轴、z轴的正方向建立空间直角坐标系,
如图,
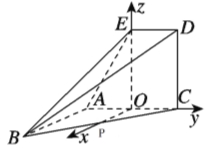
则C(0,![]() ,0),A(0,-
,0),A(0,-![]() ,0),E(0,0,
,0),E(0,0,![]() ),
),
D(0,![]() ,
,![]() ),B(a,-
),B(a,-![]() ,0).
,0).
则P(![]() ,0,0),
,0,0),
设平面EAB的法向量为![]() =(x0,y0,z0).
=(x0,y0,z0). ![]() =(a,0,0),
=(a,0,0),![]() =(0,
=(0,![]() ,
,![]() ),
),
∴![]()
![]()
![]() =0,
=0,![]()
![]()
![]() =0,
=0,
即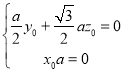 ,令z0=1,得y0=-
,令z0=1,得y0=-![]() ,又x0=0,
,又x0=0,
∴![]() =(0,-
=(0,-![]() ,1).
,1).
∴![]() ,
,
∴DP∥平面EAB (另法:取AB中点F,然后证DP∥EF或证平面ODP∥平面EAB)
(2)设平面EBD的法向量为![]() =(x1,y1,z1),易知平面ACDE的一个法向量为
=(x1,y1,z1),易知平面ACDE的一个法向量为![]() =(1,0,0).
=(1,0,0).
∵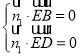 ,即
,即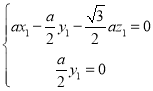 ,
,
令z1=1,则x1=![]() ,y1=0,
,y1=0,![]() =(
=(![]() ,0,1).
,0,1).
∴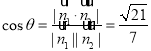 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2bx+a(a,b∈R)
(1)若a从集合{0,1,2,3}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,求方程f(x)=0恰有两个不相等实根的概率;
(2)若b从区间[0,2]中任取一个数,a从区间[0,3]中任取一个数,求方程f(x)=0没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)若直线l平行于直线l1:4x-y+1=0,求l的方程;
(2)若直线l垂直于直线l1:4x-y+1=0,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
B.?α,β∈R,使cos(α+β)=cosα+cosβ
C.向量 ![]() =(﹣2,1),
=(﹣2,1), ![]() =(﹣3,0),则
=(﹣3,0),则 ![]() 在
在 ![]() 方向上的投影为2
方向上的投影为2
D.“|x|≤1”是“x<1”的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[-3.5]=-4,[2.1]=2,已知函数![]() ,则关于函数g(x)=[f(x)]的叙述正确的是( )
,则关于函数g(x)=[f(x)]的叙述正确的是( )
A. ![]() 是偶函数B.
是偶函数B. ![]() 是奇函数
是奇函数
C. ![]() 的值域是
的值域是![]() 0,
0,![]() D.
D. ![]() 的值域是
的值域是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有8名马拉松比赛志愿者,其中志愿者![]() ,
,![]() ,
,![]() 通晓日语,
通晓日语,![]() ,
,![]() ,
,![]() 通晓俄语,
通晓俄语,![]() ,
,![]() 通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
![]() 列出基本事件;
列出基本事件;
![]() 求
求![]() 被选中的概率;
被选中的概率;
![]() 求
求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公园游园活动中有这样一个游戏项目:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和2个黑球,这些球除颜色外完全相同;每次游戏都从这两个箱子里各随机地摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中:①求摸出3个白球的概率;②求获奖的概率;
(2)在两次游戏中,记获奖次数为X:①求X的分布列;②求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com