
| 27 |
| x |
| 27 |
| x |
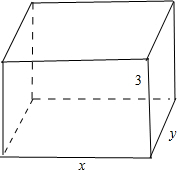 设底面的长为xm,宽ym,则y=
设底面的长为xm,宽ym,则y=| 27 |
| x |
| 27 |
| x |
| 27×6 |
| x |
4500x•
|
| 10 |
| 27×6 |
| x |
| 10 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
| A、一个命题与它的逆命题、否命题、逆否命题等四种命题中真命题个数为偶数 | ||||||||
| B、命题:“若xy=0,则x=0或y=0”的逆否命题是“若x≠0或y≠0,则xy≠0” | ||||||||
C、椭圆
| ||||||||
D、已知两条直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充分不必要条件是
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 高一年级 | 高二年级 | |
| 不支持 | 30 | 40 |
| 支持 | 160 | 270 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
| P(x2≥k) | 0.050 | 0.030 | 0.001 |
| k | 3.041 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com