练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．计算$\overrightarrow{AB}$+$\overrightarrow{CA}$-$\overrightarrow{CB}$=（　　）
    A．$\overrightarrow{AC}$B．$\overrightarrow{CA}$C．0D．$\overrightarrow{0}$

    分析 根据向量加法的几何意义，以及向量数乘的几何意义即可得出答案．

    解答 解：$\overrightarrow{AB}+\overrightarrow{CA}-\overrightarrow{CB}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}$．
    故选：D．

    点评 考查向量、向量加法，以及向量数乘的几何意义，零向量的概念．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

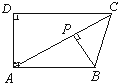    20．如图，已知四边形ABCD中AB∥CD，AD⊥AB，BP⊥AC，BP=PC，CD＞AB，则经过某种翻折后以下线段可能会相互重合的是（　　）
    A．AB与ADB．AB与BCC．BD与BCD．AD与AP

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则角C的取值范围为（　　）
    A．（0，$\frac{π}{3}$]B．[$\frac{π}{3}$，$\frac{π}{2}$）C．[$\frac{π}{6}$，$\frac{π}{3}$]D．（$\frac{π}{4}$，$\frac{π}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

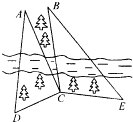    18．如图，为了开发某森林区，某测量人员身处这个森林区一条河的南岸，为了测量河对岸不能到达的两点A，B之间的距离，同时由于树木的遮挡，不可能分别在两个不同地点同时观察到点A，B；但她在南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；已知A，B，C，D，E在同一水平面内并测量得到数据：∠ACD=90°，∠ADC=60°，∠ACB=15°，∠BCE=105°，∠CEB=45°，DC=CE=1（km）．
    （I）求AB之间的距离；
    （Ⅱ）若计划由A向B建一条直线公路，再由点C处向公路AB建一条空中滑索，求滑索的最短长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在一个不透明的袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同，现从中一次摸出两个小球．
    （1）请写出所有的基本事件；    
    （2）求摸出的两个小球标注的数字之和不大于5的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

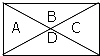    15．用5种不同的颜色给如图标有A，B，C，D的各部分涂色，每部分只涂一种颜色，且相邻两部分不同颜色，则不同的涂色方法共有（　　）
    A．160种B．240种C．260种D．360种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在（1+x）3+（1+x）4+（1+x）5+（1+x）6+（1+x）7的展开式中，x3的系数为（　　）
    A．C${\;}_{7}^{4}$B．C${\;}_{8}^{4}$C．C${\;}_{8}^{3}$D．C${\;}_{9}^{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，角A，B，C分别对应边a，b，c，已知a，b，c成等比数列，且sinB=$\frac{\sqrt{7}}{4}$；
    （Ⅰ）若$\overrightarrow{BA}•\overrightarrow{BC}=\frac{3}{2}$，求a，c的值；
    （Ⅱ）求$\frac{1}{tanA}+\frac{1}{tanC}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知集合A={x|x2≤2x}，B={y|y＞1}，则A∩B等于{x|1＜x≤2}．

    查看答案和解析>>

    同步练习册答案