
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 面
面![]() ;
;
(2)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,请计算
,若存在,请计算![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2)存在,![]() (3)
(3)![]()
【解析】
(1)可通过题干中的线段关系求出对应的各底边弦长,得到![]() ,通过线面垂直的判定定理结合
,通过线面垂直的判定定理结合![]() ,可证
,可证![]() ,又由
,又由![]() 三边关系可得
三边关系可得![]() ,进而得证;
,进而得证;
(2)可连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,利用相似三角形关系可确定点
,利用相似三角形关系可确定点![]() 应为
应为![]() 上靠近
上靠近![]() 的三等分点,进而求证;
的三等分点,进而求证;
(3)在线段![]() 上取点
上取点![]() ,使
,使![]() ,则
,则![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() 通过三垂线法得证
通过三垂线法得证![]() ,再结合等体积法
,再结合等体积法![]() ,即可求解
,即可求解![]() 到平面
到平面![]() 的距离.
的距离.
(1)∵在底面![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)存在点![]() ,当
,当![]() 时,使
时,使![]() 平面
平面![]() ,
,
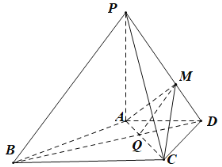
连接![]() ,交
,交![]() 于点
于点![]() ,
,
因为![]() ,所以
,所以![]() ,所以在
,所以在![]() 中,要使
中,要使![]() ,则
,则![]() 即可,所以,在
即可,所以,在![]() 上存在点
上存在点![]() ,当
,当![]() 时
时![]() 平面
平面![]()
(3)在线段![]() 上取点
上取点![]() ,使
,使![]() ,则
,则![]() ,
,
又由(1)得![]() 平而
平而![]() ,
,![]() 平面
平面![]() ,
,
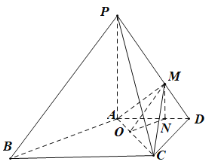
又![]() 平面
平面![]() ,
,![]() ,
,
作![]() 于
于![]() ,连接
,连接![]()
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() 得
得![]() .
.
∴点![]() 到平面
到平面![]() 的距离
的距离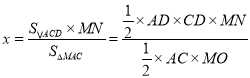
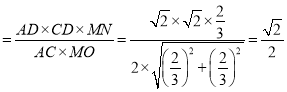 .
.


科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟).
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 34 | 51 | 59 | 66 | 65 | 25 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 40 | 160 | |
合计 |
(2)通过计算判断,是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关?
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019年”是一个重要的时间节点——中华人民共和国成立70周年,和全面建成小康社会的 关键之年.70年披荆斩棘,70年砥砺奋进,70年风雨兼程,70年沧桑巨变,勤劳勇敢的中国 人用自己的双手创造了一项项辉煌的成绩,取得了举世瞩目的成就.趁此良机,李明在天猫网店销售“新中国成立70周年纪念册”,每本纪念册进价4元,物流费、管理费共为![]() 元/本,预计当每本纪念册的售价为
元/本,预计当每本纪念册的售价为![]() 元(
元(![]() 时,月销售量为
时,月销售量为![]() 千本.
千本.
(I)求月利润![]() (千元)与每本纪念册的售价X的函数关系式,并注明定义域:
(千元)与每本纪念册的售价X的函数关系式,并注明定义域:
(II)当![]() 为何值时,月利润
为何值时,月利润![]() 最大?并求出最大月利润.
最大?并求出最大月利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 斜率为
斜率为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 上的一点
上的一点![]() 作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足
作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足![]() ,
,![]() ,线段QD与
,线段QD与![]() 交于点P.
交于点P.

(1)当点P在抛物线C上,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com