练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数．

    （1）求函数的最小正周期、最小值、对称轴、对称中心；

    （2）设的内角的对边分别为，且，若，求的值．

    【答案】(1) 最小正周期是，最小值是-2. 对称轴为；对称中心为；(2) .

    【解析】

    (1)先根据两角和与差的正弦公式化简为 的形式,结合正弦函数的最值,对称轴和对称中心可得到函数 的最小值,对称轴和对称中心,再由 可求出其最小正周期.

    (2)由(1)确定的的解析式及,求出.由的范围,求出的范围,利用特殊角的三角函数值及正弦函数的图象求出角的度数,由,利用正弦定理得到,再利用余弦定理得到,将与的值代入得到关于和的方程求出与的值.

    解：（1）∵=,

    ∴的最小正周期是，最小值是-2.

    令，则的对称轴为,

    令，则的对称中心为,

    （2）,则=1,

    ,,

    ,解得,

    又，由正弦定理得 ①,

    由余弦定理得，即3= ②,

    由①②解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

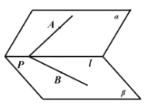
    【题目】如图，二面角中，，射线，分别在平面，内，点A在平面内的射影恰好是点B，设二面角、与平面所成角、与平面所成角的大小分别为，则（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）若关于的不等式在上恒成立，求的取值范围；

    （Ⅱ）设函数，在（Ⅰ）的条件下，试判断在上是否存在极值．若存在，判断极值的正负；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某冰糖橙，甜橙的一种，云南著名特产，以味甜皮薄著称。该橙按照等级可分为四类：珍品、特级、优级和一级（每箱有5kg）,某采购商打算订购一批橙子销往省外，并从采购的这批橙子中随机抽取100箱，利用橙子的等级分类标准得到的数据如下表：

    等级

    珍品

    特级

    优级

    一级

    箱数

    40

    30

    10

    20

    （1）若将频率改为概率，从这100箱橙子中有放回地随机抽取4箱，求恰好抽到2箱是一级品的概率：

    （2）利用样本估计总体，庄园老板提出两种购销方案供采购商参考：

    方案一：不分等级卖出，价格为27元/kg;

    方案二：分等级卖出，分等级的橙子价格如下：

    等级

    珍品

    特级

    优级

    一级

    售价（元/kg）

    36

    30

    24

    18

    从采购商的角度考虑，应该采用哪种方案？

    （3）用分层抽样的方法从这100箱橙子中抽取10箱，再从抽取的10箱中随机抽取3箱，X表示抽取的是珍品等级，求x的分布列及数学期望E（X）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号．某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据（=1,2，…，6），如表所示：

    试销单价（元）

    4

    5

    6

    7

    8

    9

    产品销量（件）

    q

    84

    83

    80

    75

    68

    已知．

    （Ⅰ）求出的值；

    （Ⅱ）已知变量具有线性相关关系，求产品销量（件）关于试销单价（元）的线性回归方程；

    （参考公式：线性回归方程中，的最小二乘估计分别为,)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，且，.

    （1）证明：面；

    （2）在上是否存在点，使平面，若存在，请计算的值，若不存在，请说明理由；

    （3）若，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (其中e是自然对数的底数，k∈R)．

    (1)讨论函数的单调性；

    (2)当函数有两个零点时，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求f（x）的单调区间；

    （2）若当时，不等式f （x）＜m恒成立，求实数m的取值范围；

    （3）若关于x的方程f（x）＝x2+x+a在区间[0，2]上恰好有两个相异的实根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两品牌计划入驻某商场，该商场批准两个品牌先进场试销天。两品牌提供的返利方案如下：甲品牌无固定返利，卖出件以内（含件）的产品，每件产品返利元，超出件的部分每件返利元；乙品牌每天固定返利元，且每卖出一件产品再返利元。经统计，两家品牌在试销期间的销售件数的茎叶图如下：

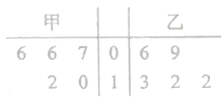
    （Ⅰ）现从乙品牌试销的天中随机抽取天，求这天的销售量中至少有一天低于的概率.

    （Ⅱ）若将频率视作概率，回答以下问题：

    ①记甲品牌的日返利额为（单位：元），求的分布列和数学期望；

    ②商场拟在甲、乙两品牌中选择一个长期销售，如果仅从日返利额的角度考虑，请利用所学的统计学知识为商场作出选择，并说明理由.

    查看答案和解析>>

    同步练习册答案