
【题目】已知函数![]() (其中e是自然对数的底数,k∈R).
(其中e是自然对数的底数,k∈R).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当函数![]() 有两个零点
有两个零点![]() 时,证明:
时,证明: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
本题考查导数与函数单调性的关系以及用导数证明不等式的问题。(1)求导数后,根据导函数的符号判断出函数的单调性。(2)根据题意将证明![]() 的问题转化为证明
的问题转化为证明![]() ,即证
,即证![]() ,构造函数
,构造函数![]() ,
,
利用函数![]() 的单调性证明即可。
的单调性证明即可。
试题解析:
(1)解:∵![]()
∴![]() 。
。
①当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增。
单调递增。
②当![]() 时,
时,![]() 恒成立,
恒成立,
∴函数![]() 在R上单调递增.
在R上单调递增.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增。
上单调递增。
当![]() 时,
时,![]() 在R上单调递增.
在R上单调递增.
(2)证明:当![]() 时,由(1)知函数
时,由(1)知函数![]() 单调递增,不存在两个零点。
单调递增,不存在两个零点。
所以![]() 。
。
设函数![]() 的两个零点为
的两个零点为![]() ,
,
则![]() ,
,
设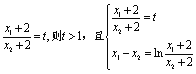 ,
,
解得![]() ,
,
所以![]() ,
,
要证![]() ,
,
只需证![]() ,
,
设![]()
设![]() 单调递增,
单调递增,
所以![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,
,
故![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,C1的参数方程为 (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(Ⅰ)说明C2是哪种曲线,并将C2的方程化为普通方程;
(Ⅱ)C1与C2有两个公共点A,B,定点P的极坐标![]() ,求线段AB的长及定点P到A,B两点的距离之积.
,求线段AB的长及定点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
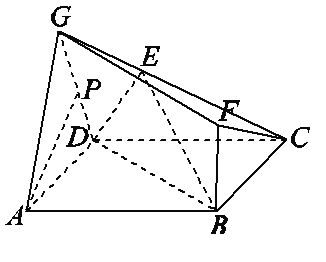
【题目】如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,BF⊥平面ABCD,∠GDC=90°,点E是线段GC上除两端点外的一点,若点P为线段GD的中点.
(Ⅰ)求证:AP⊥平面GCD;
(Ⅱ)求证:平面ADG∥平面FBC;
(Ⅲ)若AP∥平面BDE,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点
经过点 ,离心率为
,离心率为![]() .
.
(1)求椭圆E的标准方程;
(2)若A1,A2分别是椭圆E的左、右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),连接PA1交直线l于点B,点Q为线段A2B的中点,求证:直线PQ与椭圆E只有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点![]() ,抛物线上的点
,抛物线上的点![]() ,过点B作直线AP的垂线,垂足为Q.
,过点B作直线AP的垂线,垂足为Q.
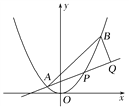
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,,AC=AD=CD,E是AD的中点.
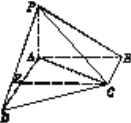
(Ⅰ)证明CE∥平面PAB;
(Ⅱ)证明:平面PAD⊥平面PCE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.

(Ⅰ)求证:平面AB1M⊥平面A1ABB1;
(Ⅱ)过点C作一截面与平面AB1M平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),长轴长为4,离心率为
(a>b>0),长轴长为4,离心率为![]() .
.
(Ⅰ)椭圆的求椭圆的标准方程;
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为![]() ,第二小组频数为12.
,第二小组频数为12.
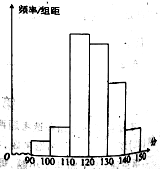
(Ⅰ)求第二小组的频率及抽取的学生人数;
(Ⅱ)若分数在120分以上(含120分)才有资格被录取,约有多少学生有资格被录取?
(Ⅲ)学校打算从分数在![]() 和
和![]() 分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在
分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在![]() 分的学生的概率.
分的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com