
分析 由题意可得|$\overrightarrow{c}$|≤|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|,故当且仅当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|取得最小值为2$\sqrt{2}$,从而求得|$\overrightarrow{c}$|的最大值.
解答 解:设$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,若$\overrightarrow c$满足|${\overrightarrow c$-(${\overrightarrow a$+$\overrightarrow b}$)|=|${\overrightarrow a$-$\overrightarrow b}$|≥|$\overrightarrow{c}$|-|$\overrightarrow{a}$+$\overrightarrow{b}$|,即|$\overrightarrow{c}$|≤|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|,
当且仅当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|取得最小值为2$\sqrt{2}$,
∴|$\overrightarrow{c}$|的最大值为2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题主要考查了向量模的运算性质、向量的平行四边形法则及其向量垂直的性质的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (A∪B)∪C=U | B. | (A∪B)∩C=∅ | C. | (A∩B)∩C=∅ | D. | (A∩B)∪C=C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
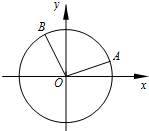 如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点A,B.若点A的横坐标是$\frac{3\sqrt{10}}{10}$,点B的纵坐标是$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点A,B.若点A的横坐标是$\frac{3\sqrt{10}}{10}$,点B的纵坐标是$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com